построим прямую OA от точки O до прямой MH так что угол OAM = 90 градусов,
это и есть расстояние от точки O до прямой MН
Треугольники MOA и MOK равны это следует из следующего :
1 в треуг ОАМ угол OAM = 90 гр
в треуг OMK угол OKM = 90 гр
2 угол АMO = углу KMO (биссектриса угла)
3 сторона треугольника MO общая для обоих треугольников
4 также угол MOA и угол MOK в обоих треуг. равны, поскольку
сумма углов в треуг. = 180 гр. ( вычитая 180 - 90 гр - известный угол)
Этих условий достаточно чтобы сделать вывод, что треугольники равны.
Следовательно OK = OA = 9
ответ 9
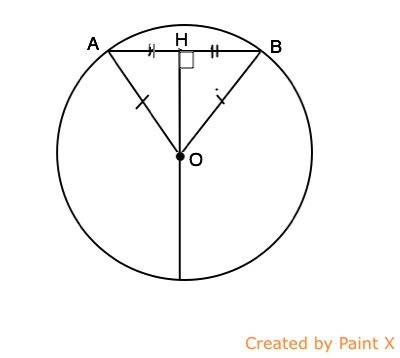
Соединим центр О окружности с концами хорды АВ. ОА=ОВ=R.
Треугольник АОВ - равнобедренный. Проведем высоту ОН этого треугольника.
Угол ОНВ=углу ОНА=90º
«Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один»
Следовательно, и к середине хорды можно провести только один перпендикуляр.
Высота ОН - медиана равнобедренного треугольника.
АН=ВН. Точка Н - середина АВ.
Следовательно, ОН, проходящий через середину АВ, есть срединный перпендикуляр хорды АВ, ч.т.д.
ответ
6
Объяснение
Т.к медиана делит сторону на 2 равные части, нужно просто 3*2