Объяснение:
3 задача
так как 1 угол равен 90 градусов, то это прямоугольный треугольник.
в прямоугольном треугольнике катет лежащий против угла 30 градусов равен половине гипотенузы.
PD=1,2см и лежит напротив угла Q(30 градусов) значит PD равен половине гипотенузы(наибольшая сторона треугольника - PQ), значит PQ = 2PD
PQ = 1,2 * 2 = 2,4
4 задача
так как 1 угол равен 90 градусов, то это прямоугольный треугольник.
обратное свойство прямоугольного треугольника: если катет(сторона) равен половине гипотенузы(наибольшая сторона треугольника), то он(катет) лежит против угла 30 градусов.
AB = 4,2см это половина гипотенузы(CB), значит AB лежит против угла 30 градусов, то есть угол C равен 30 градусов.
Нужно найти угол B.
можно использовать два
первый
сумма всех углов треугольника равна 180 градусов. Чтобы найти угол B нужно вычесть из 180 градусов угол A(90 градусов) и угол C(30 градусов) получаем, что угол B = 60 градусов
второй
в прямоугольном треугольнике один угол равен 90 градусов, и сумма двух других равна 90 градусов.
значит нужно из 90 градусов вычесть угол C(30 градусов) значит угол B равен 60 градусов
Задача: Вне плоскости прямоугольника ABCD взяты точки M, причем MA⊥AB и MA⊥AD. Найти градусную меру угла между прямой MC и плоскостью ABC, если AB = 1 см, AD = √2 см, AM = 1 см.
ΔAMC — прямоугольный, ∠MAC = 90°, т.к. MA⊥AB и MA⊥AD ⇒ MA⊥ABCD и MA⊥ABC.
AC — диагональ ABCD и проекция MC на плоскость ABC.
∠ACM — угол между прямой MC и плоскостью ABC.
AD = BC = √2 см; AB = CD = 1 см, т.к. ABCD — прямоугольник.
Найдем AC за т. Пифагора:
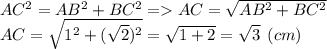
Найдем MC за т. Пифагора:
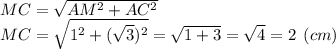
Если катета меньше за гипотенузу в два раза, он лежит напротив угла в 30°. Катет AM =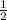 
MC ⇒ ∠ACM = 30°.
ответ: Градусную меру угла равна 30°.
Угол А образован векторами АВ и АС. Находим их координаты, вычитая от координаты конечной точки кооординаты начальной.
AB = {3-3;2-(-1)} = {0;3}.
AC = {-1-3;-2-(-1)} = {-4;-1}.
cosA = (0*(-4) + 3*(-1)) / (√(0²+3²) * √((-4)²+(-1)²) = -3 / (3√17) = -1/√17 ≈-0.2425. ∠A = 104°. И про другие углы аналогично.
Объяснение: