
ответ:Древняя задача.
Объяснение: Полагаю речь идет о разделении угла с линейки без делений и циркуля.
1. На два угол делится просто - надо построить биссектрису.
Строится она легко.
а. Выставить произвольный раствор циркуля
2. Отметить на сторонах угла отрезки, равные раствору циркуля ОА и ОВ.
3. С центром в точках А и В построить дуги, которые пересекаются.
4. Точка О и получившаяся точка пересечения дают луч, который и есть биссектриса.
Древняя задача о делении угла на 3 равных части решается только в некоторых случаях, общего решения не существует.
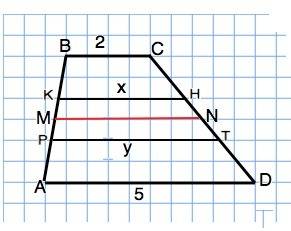
Обозначим трапецию АВСD.
Точки Н и Т делят сторону СD на отрезки
СН=НТ=ТD.
Теорема Фалеса. Если на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. ⇒
ВК=КР=РА.
Средняя линия трапеции АВСD - отрезок МN=(ВС+AD):2=(2+5):2=3,5 (м)
СH=HT=TD ⇒
HN=NT, поэтому
MN- средняя линия трапеции РКНТ.
Примем КН=х, РТ=у
Тогда х+у=2•3,5=7, откуда
у=7-х.
КН- средняя линия трапеции РВСТ
КН=(2+(7-х)):2=х
9-х=2х ⇒
х=3 (м) - длина отрезка КН
у=7-3=4 (м) - длина отрезка РТ
АВ =25,ВС= 30; BD - перпендикуляр проведенный к плоскости.
АB и ВС - проекции,т.к наклонная ВС больше АВ,то и проекция СD большеАD следовательно
CD - AD = 11.
Пусть проекция AD будет х,тогдаСD = x +11,
т.Пифагора: ВD²= AB² - AD²
BD² = BC²- ÇD² значит
АВ² - АD² = BC² - CD²
. x = 11, x + 11 = 29
снова используется т.Пифагора:
ВD² = AB²- AD²
BD²= 625 -324
BD² = 301
2.
ab =13,ac=15: BC =14: EO = 20
EO перпендикуляр к ВС, т.к это кратчайшее расстояние к ВС.
АО - проекция ЕО на плоскость ∆ АВС.
Углы АОС и АОВ= 90°
Рассмотрим ∆ АОС и ∆ АОВ, с общим катетом АО;
по т Пифагора найдем катет каждого ∆
АО² = АВ² - ВО²
АО² = АС² - ВО²,тогда
АВ² - (14- СО)²= АС²- СО²
13² - (14 - СО)² = 15² - СО
13² - 14² + 28 × СО - СО²= 15² - СО²
28× СО = 196 +225-169
СО =252/28
СО = 9, тогда ВО = 14 - 9 = 5
теперь найдем АО² = АВ² - ВО² = 13² - 5²= 144: АО = 12
теперь определим величину отрезка АЕ
АЕ² = ЕО² - АО²= 20² -12² = 400 - 144 =256
АЕ = 16