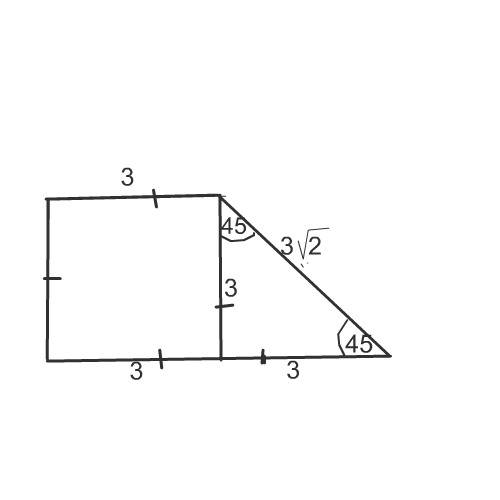
Сделаем рисунок к задаче.
Высота этой трапеции отсекает от нее прямоугольный равнобедренный треугольник с гипотенузой 3√2.
Такой треугольник - половина квадрата с диагональю=гипотенузе.
Формула диагонали квадрата ( формула гипотенузы равнобедренного прямоугольного тр-ка).
d=а√2, где а- сторона квадрата, а в равнобедренном прямоугольном треугольнике - катет. Знание этой формулы часто избавляет от лишних вычислений.
d=СК
СК =3√2=СН√2
СН√2=3√2
СН=3 см
СН=НК как равный катет.
АК=2НК
ВС=АК:2
Площадь трапеции равна Н*(АВ+ВС)
S=3*(3+6):2=13,5 см²
1. Переведем метры в сантиметры: a=6м=600см, b=8м=800см. Зная стороны, можно найти периметр участка: 2(a+b)=2*600+2*800=1200+1600=2800см. 2800см/10см=280 штук.
2. Представим меньшую сторону прямоугольника, как x. Тогда большая сторона будет равна 2,5x. Следовательно,
x*2,5x=250
2,5x²=250
x²=100
x=10см. Из этого следует, что 2,5x=25см.
3. Площадь прямоугольника S=8*18=144. S прямоугольника = S квадрата, S квадрата = a², значит a=12см
4. Площадь трапеции равна произведению высоты на полусумму оснований:
S=h*(a+b)/2
Высота этой трапеции является катетом прямоугольного треугольника и противолежит углу 30°, поэтому равен половине гипотенузы – стороны трапеции, к которой этот угол прилежит.
h=36/2=18см
S=18*(45+68)/2=18*113=1017см²
Объяснение:
Даны прямые а и b.
Нужно на прямой а построить точку (пусть это будет точка М), расстояние от которой до прямой b будет равно длине отрезка PQ,
Известно, что расстояние от точки до прямой равно длине перпендикуляра, проведенного из этой точки к данной прямой.
Построим на прямой b перпендикуляр по общеизвестному начертим две пересекающиеся окружности одинакового произвольного радиуса с центрами на прямой b, точки пересечения соединим и получим перпендикуляр.
На этом перпендикуляре отложим ТЕ=длине отрезка PQ.
Через точку Е проведем параллельно прямой b прямую до пересечения с прямой а. ( Это сделаете так же, как строили перпендикуляр к b)
Так как расстояние между всеми точками параллельных прямых одинаково, точка М на прямой а и есть искомая точка.
Расстояние от нее до прямой b равно длине отрезка PQ