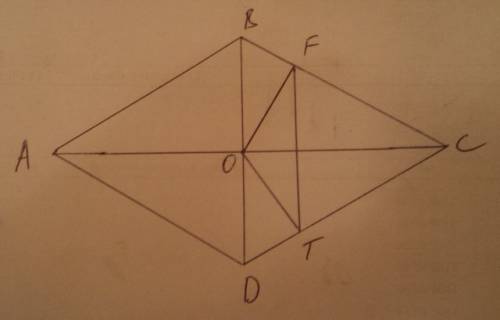
Итак, раз в условии сказано что BD равна стороне DA значит треугольник DВС равносторонний (у ромба все стороны равны). У равностороннего треугольника все углы равны 60 градусам, слудовательно угол СВD = 60 градусам. Поскольку треугольник ОFВ прямоугольный (ОF перпендткуляр к ВС), то значит угол FОВ = 180-90-60=30 градусов. Поскольку угол ВОС прямой, то угол FОС = 90-30 = 60 градусов. Т.к. угол ТОС = FОС, то угол FОТ = 2 * FОС = 2*60=120 градусов.
Если ОF и ОТ перпендикуляры (по условию задачи), значит они равны, следовательно треугольник FОТ - равносторонний. У равностороннего треугольника углы у основания равны. Значит угол ОFТ= углу ОТF и равен (180-120)/2=30 градусов.
ответ FОТ = 120 градусов, ОFТ= ОТF = 30 градусов
Площадь боковой поверхности наклонной призмы равна сумме площадей ее граней.
Площади двух граней даны в условии. Необходимо найти площадь третьей грани и сложить все площади.
Площадь грани призмы - это площадь параллелограмма, которая равна произведению высоты на сторону, к которой она проведена.
Длина стороны у всех граней одинакова - это длина ребра призмы и равна 5 см.
Высота грани АА1СС1, площадь которой пока еще неизвестна, - это катет ас прямоугольного треугольника abc, образованного высотами граней призмы, так как
угол между гранями АА1СС1 и СС1В1В прямой по условию .
Чтобы найти высоту грани АА1СС1 (катет aс треугольника abc),
нужно найти высоты граней, площади которых известны
(найти катет bc и гипотенузу ac прямоугольного треугольника abc)
Из площади грани СС1В1В =50 см² найдем ее высоту (катет cb):
cb=50:5=10 см
Из площади грани АА1В1В=130 см² найдем ее высоту (гипотенузу аb):
аb=130:5=26 см
Высоту ас третьей грани найдем по теореме Пифагора:
aс²=ab²-cb²
ас=√(676-100)=√576=24 см
Площадь третьей грани равна
24*5=120 см²
Sбоковая=120+130+50=300 см²