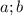 . И пусть
. И пусть 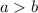 тогда большая высота опускается на меньшую сторону , меньшая на большую . Тогда площадь с одной стороны равна
тогда большая высота опускается на меньшую сторону , меньшая на большую . Тогда площадь с одной стороны равна 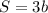 , с другой стороны
, с другой стороны 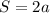 .
.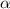 тогда острый угол равен
тогда острый угол равен 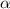 следовательно тупой
следовательно тупой 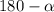 . Из прямоугольных треугольников которые образовались после проведения высота соответственно на стороны
. Из прямоугольных треугольников которые образовались после проведения высота соответственно на стороны 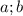 равны
равны 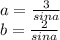 тогда площадь запишится как
тогда площадь запишится как 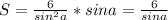
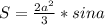 приравняем
приравняем 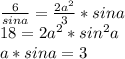 -3 нам не подходит потому что синус в
-3 нам не подходит потому что синус в  четверти положителен
четверти положителен 
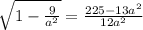 решая это уравнение получим
решая это уравнение получим 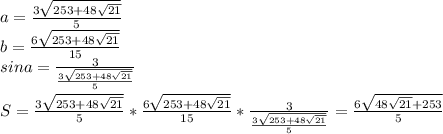

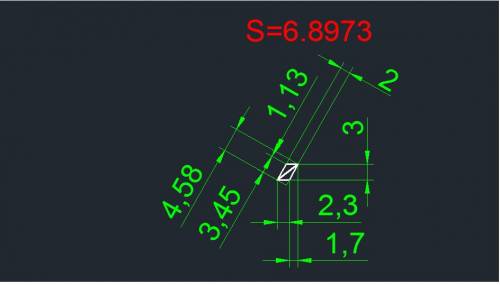
(0; 1) и (-1; 0)
Объяснение:
x² - 2xy + 2x - y + 1 = 0
Преобразуем уравнение
(х² + 2х + 1) - у(2х + 1) = 0
(х + 1)² - у(2х + 1) = 0
у = (х + 1)² : (2х + 1)
или
у = 1 + х²/(2х + 1)
По условию отношение х²/(2х + 1) = k ( k - целое число)
х² = 2кх + k
х² - 2кх - k = 0
Единственное решение имеет место, если дискриминант равен нулю
D = 4k² + 4k = 0
k = 0 и k = - 1
Итак, мы получили
х²/(2х + 1) = 0 ⇒ х = 0 ⇒ у = 1 + х²/(2х + 1) = 1
х²/(2х + 1) = -1 ⇒ х = -1 ⇒ у = 1 + х²/(2х + 1) = 0
Итак
при х = 0 у = 1 - 1--е целочисленное решение
а при х = -1 у = 0 - 2-е целочисленное решение