76°
Объяснение:
Признак равнобедренного треугольника: если в треугольнике два угла равны, то такой треугольник - равнобедренный.
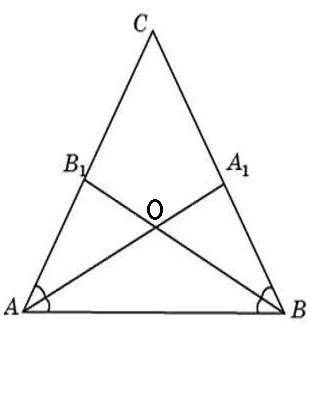
1) Рассмотрим ΔАСВ.
∠С =28°, ∠А = ∠В по условию. Т.к. сумма углов 28° Δ-ка равна 180°, то?
∠А + ∠В + ∠С = 180°, откуда
∠А + ∠В = 180° - ∠С = 180° - 28° = 152°. Но ∠А = ∠В по условию, следовательно,
∠А = ∠В = 152°/2 = 76°
2) т.к. ∠А = ∠В , а АА₁ и ВВ₁ - биссектрисы этих углов, то
∠В₁АО = ∠ОАВ = ∠А₁ВО=∠ОВА = 76°/2 = 38°
3) Рассмотрим ΔАОВ.
∠ОАВ = ∠ОВА =38°, тогда
∠АОВ = 180° -2*38° = 180° -76° = 104°
4) ∠АОВ и ∠АОВ₁ - смежные углы, их сумма = 180°, значит,
∠АОВ₁ = 180°-104° = 76°
Так как CH биссектриса, то она делит угол на 2 равные части, то есть 120:2=60.
Мы знаем, что биссектриса образовывает угол в 90 градусов, угол H= 90, найдем угол А. Сумма углов треугольника = 180, чтобы найти угол А надо из 180 вычесть 90 и 60= 30 градусам. Катет лежащий против угла в 30 градусов равен половине гипотенузы CH= 12:2 = 6 см