
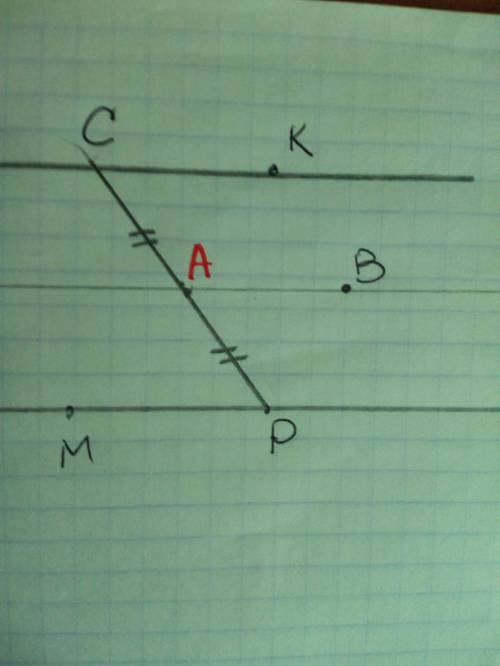
1. Расположим АВ между параллельными СК и МР. Соединим С и Р, возьмем середину этого отрезка - точку А.
Проведим через нее прямую АВ, она не может совпадать с СК, т.к. СК и МВ по условию параллельны, т.е. не имеют общих точек. СК параллельна и АВ по условию. Значит, АВ параллелльна МР. Если прямая параллельна двум прямым, то эти две прямые параллельны между собой. МР параллельна СК. Да, собственно, это и по условию сказано.)
Картинку прикрепил.
2. Указанные в задании углы являются соответственными. правда, прямые не параллельны, но углы эти здесь и не равны.
3. Указанные углы смежные, и образуют развернутый угол в 180°
Пусть сторона ромба с две полудиагонали образуют прямоугольный треугольник АВС с катетами АС и ВС.
Найдём сторону ромба (это АС).
АС = √(144² + 42²) = √(20736 + 1764) = √22500 = 150.
Площадь треугольника можно записать двумя разными как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту h.
То есть:
h*150 = 42*144.
Отсюда искомая величина равна:
h = 42*144/150 = 6048 / 150 = 1008 / 25 = 40,32.