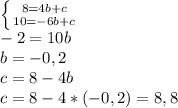

∠АОВ и ∠COD вертикальные,
∠ВОС и ∠AOD вертикальные.
Проведем:
ОЕ - биссектрису ∠АОВ,
OF - биссектрису ∠СOD,
OK - биссектрису ∠BOC,
OM - биссектрису ∠AOD.
Сначала докажем, что биссектрисы смежных углов перпендикулярны.
∠ВОА и ∠ВОС смежные, значит их сумма равна 180°:
∠1 + ∠2 + ∠3 + ∠4 = 180°
Биссектрисы разбили эти углы на пары равных углов:
∠1 = ∠2 и ∠3 = ∠4, значит
2 ·∠2 + 2 ·∠3 = 180°
2(∠2 + ∠3) = 180°
∠2 + ∠3 = 90°, значит
ОЕ⊥ОК.
∠СОВ и ∠COD смежные, значит и их биссектрисы пересекаются под прямым углом:
OF⊥OK.
Углы ЕОК и FOK имеют общую сторону ОК и составляют в сумме 180°, значит они смежные, следовательно стороны ОЕ и OF являются дополнительными лучами, т.е. лежат на одной прямой.
Что и требовалось доказать.
Окружностью называется фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки.
Круг- геометрическое место точек плоскости, растояние от которых до данной точки, называемой центром круга, не перевышает заданного неотрицательного числа, называемого радиусом этого круга.
Биссектриса- прямая которая делит угол пополам
Медиана- прямая которая делт сторону пополам.
Высота- перпендиуляр опущеный из вершины угла к противополож. строне.
Диаметр- хорда которая проходит через центр окружности
Хорда- прямая соединяющая две точки окружности
Радиус- растояние от точки окружности до ее центра.