Задача решена Пользователем Рисадес Хорошист
Исправлена неточность в последнем действии.
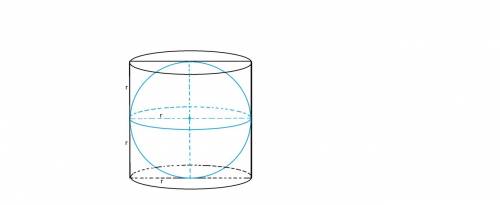
Шар может быть вписан в цилиндр только тогда, когда этот цилиндр правильный, т.е. когда его осевое сечение является квадратом.
Радиус основания цилиндра равен радиусу шара и равен r.
Высота цилиндра равна диаметру основания и равна 2 r.
Полная площадь поверхности складывается из площади двух оснований и площади боковой поверхности:
2*πr² + 2πr*2r = 6πr²
Площадь шара = 4πr²
Площадь цилиндра больше площади шара в
6πr² : 4πr² = 1,5 (раза)
Площадь полной поверхности шара
111 : 1,5 = 74 ( единиц площади)
Объяснение:
Основная формулировка содержит алгебраические действия — в прямоугольном треугольнике, длины катетов которого равны {\displaystyle a}a и {\displaystyle b}b, а длина гипотенузы — {\displaystyle c}c, выполнено соотношение:
{\displaystyle a^{2}+b^{2}=c^{2}}a^{2}+b^{2}=c^{2}.
Возможна и эквивалентная геометрическая формулировка, прибегающая к понятию площади фигуры: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. В таком виде теорема сформулирована в Началах Евклида.
Обратная теорема Пифагора — утверждение о прямоугольности всякого треугольника, длины сторон которого связаны соотношением {\displaystyle a^{2}+b^{2}=c^{2}}a^{2}+b^{2}=c^{2}. Как следствие, для всякой тройки положительных чисел {\displaystyle a}a, {\displaystyle b}b и {\displaystyle c}c, такой, что {\displaystyle a^{2}+b^{2}=c^{2}}a^{2}+b^{2}=c^{2}, существует прямоугольный треугольник с катетами {\displaystyle a}a и {\displaystyle b}b и гипотенузой {\displaystyle c}c.