Точка М равноудалена от АС и ВС, т.е. находится на равном от этих сторон расстоянии.
Расстояние от точки до прямой измеряется длиной орезка, проведенного перпендикулярно.
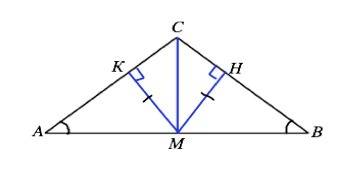
МК⊥АС, МН⊥ВС и КМ=МН
В прямоугольных ∆ АКМ и ∆ ВНМ равны острые углы А = В ( углы при основании равнобедренного треугольника), значит, равна и другая пара острых углов: ∠КМА=∠НМВ.
Катет КМ=катету МН ( по условию)
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.=>
∆ АКМ =∆ ВНМ , следовательно, АМ=ВМ.
∆ АМС = ∆ ВМС по двум сторонам и углу между ними. =>
∠СМА=∠СМВ, они смежные и равны 180°:2=90° .⇒
СМ - проведена из вершины угла треугольника к противоположной стороне, перпендикулярна ей, следовательно, СМ - высота треугольника АВС
СКазКа о веселом Сообществе.)
В некоторой премудрой-прелестной математической плоскости
жили - поживали две подружки , две Точки А и В. Через эти точки пробегало бесконечное множество дорог и тропинок, и каждый, житель этой плоскости, следуя мимо подружек, то и дело, спотыкался. Худо - бедно, но дожили до старости точки. А дело близилось к закату, решили они организовать сообщество, так и назвав его ПРЯМАЯ, потому как если вместе, весело объединиться, так никто не тронет.) К тому же, через две различные, подчеркиваю, различные точки, проходит одна и только одна прямая, а уж куда дальше приведет дорога, об этом в следующей сказке. Засыпай, малыш, пусть тебе приснится еще ни одна аксиома под мирным небом.
Против угла в 30 градусов лежит катет равный половине гипотенузы.
Применим это правило в обратную сторону, так как гипотенуза в задаче в два раза больше катета=> Угол B=30 градусов.
A= 180=90=30=60
ответ: Угол A=60 градусов.
Если вам понравилось моё решение пометьте как лучшее