25.
тр. BCF и тр. BDC
общая сторона BC, 2 равных угла. равны по 2 признаку равенства.
тр. ABE и тр. BCD. 2 равных стороны, равные углы между ними. равны по 1 признаку равенства.
тр. ABE и тр. FBC равны, тк предыдущие треугольники тоже равные.
26.
тр AMB и тр. DNC равны по 3м сторонам. По 3 признаку.
тр. ADM и BNC равны по 3м сторонам, 3 признак.
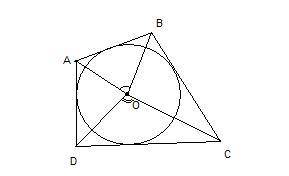
27.
тр. EDO и тр COF по двум сторонам и углу между ними, 1 признак равенства.
тр. AEO и тр FOB равны по 2м прилежащим углам и стороне. 2 признак
тр. AOD и COB равны, тк предыдущение тр. тоже равны.
28.
тр DEC и тр AFB равны по трем сторонам, 3 признак.
тр FCB и тр. DEA равны по трем сторонам, 3 признак.
29.
тр ADF и тр BEC равны по 2м сторонам и углу между ними. углы равны, тк накрестлежащие. 1 признак
боковые равны по трем сторонам, 3 признак.
31. боковые треугольники равны по 2м сторонам и углу между ними. 1 признак равенства.
32. тр DEO и тр COF равны по 2м сторонам и углу между ними, 1 признак.
боковые равны по 2м сторонам и углу между ними, 1 признак.
1. watched. 2. had. 3. shouted. 4. sent. 5 went. 6. learnt. 7. complained. 8. understood.