Пусть боковая сторона равна х,а основание равно у
Р=2х+у
15,6=2х+у
1.основание у меньше боковой стороны х на 3 м
Получается у=х-3
Подставим в первое уравнение 15,6=2х+(х-3) 15,6=2х+х-3
Решаем уравнение 3х=15,6+3 3х=18,6 х=6,2 м
У=х-3 у=6,2-3=3,2м
ответ:Основание=3,2 м боковая сторона=6,2м
2.основание у больше боковой стороны х на 3 м
Получается у=х+3
Подставим также в первое уравнение 15,6=2х+х+3 15,6-3=3х
3х=12,6 х=4,2м
У=х+3 у=4,2+3=7,2м
ответ:Основание=7,2м боковая сторона=4,2м
РЕШЕНИЕ
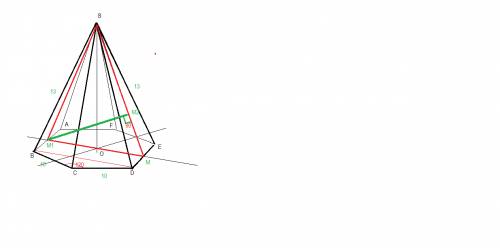
сделаем построение по условию
построим осевое сечение пирамиды ∆SMM1 , где M - середина ED ; M 1- середина AB
точка О - проекция высоты на основание ; центр отрезка ММ1 ; M1O=OM
М1М2 - высота ∆SMM1 на боковую сторону ; SM - это расстояние между прямыми SM и AB
апофема SM перпендикулярна стороне основания DE , в свою очередь DE || AB , следовательно
угол между прямыми SM и AB равен 90 град
длина апофемы по теореме Пифагора SM^2 = SE^2 - ME^2 = SE^2 - (DE/2)^2
SM = √ (13^2 - (10/2)^2) = √144 =12 см
∆BCD -равнобедренный BC=CD=10 см ; < BCD =120 град
по теореме косинусов BD^2 =BC^2+BD^2 -2*BC*BD*cosBCD =10^2+10^2-2*10*10*cos120=300 ; BD =10√3 см
MM1 = BD =10√3 см ; ОМ = M1M / 2 =10√3 /2 =5√3 см
по теореме Пифагора высота SO = √ (SM^2 - OM^2) = √ (12^2 -(5√3 )^2 ) =√69
запишем площадь сечения ∆SMM1 - двумя приравняем S
1/2 *M1M2*SM = 1/2*SO*M1M
M1M2*SM = SO*M1M
M1M2 = SO*M1M / SM = √69 * 10√3 / 12 = 5√23 / 2 см
ОТВЕТ расстояние =5√23/2 см ; угол =90 град
1) Точки B и C равноудалены от прямой AD, значит, S(abd) = S(acd).
2) Тогда S(abn) = S(abd) - S(and) = S(acd) - S(and) = S(cnd).
3) Отсюда, площади треугольников ABN и NCD равны.
Что и требовалось доказать.