Доказательство в объяснении.
Объяснени
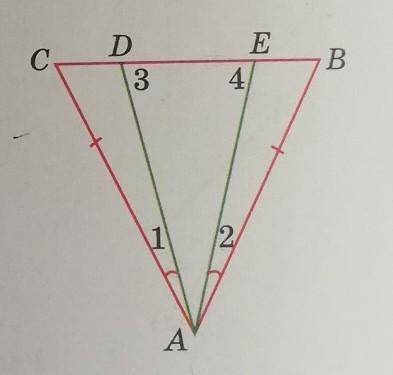
Треугольники АВМ и КСD равны по двум сторонам (АВ = CD, как противоположные сьороны параллелограмма ABCD, АМ = КС, как половины равных сторон BC и AD параллелограмма ABCD) и углу между ними (∠А = ∠С, как противоположные углы параллелограмма ABCD). Из равенства треугольников ВМ = KD.
Тогда четырехугольник BKDM - параллелограмм по признаку: "Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм", твк как ВК = MD (половины равных сторон AD и ВС), а ВМ = KD - доказано выше.
В параллелограмме BKDM диагонали точкой пересечения делятся пополам (свойство), что и требовалось доказать.
Зная градусные меры двух углов, мы можем найти третий угол: 180-90-60=30 (градусов) - угол В
У нас прямоугольный треугольник. Заметим, что угол В=30 градусов, по теореме, на против угла в 30 градусов лежит сторона равная половине гипотенузы, т.е. катет АС=1\2 АВ = 0.5*8=4
Чтобы найти неизвестный катет воспользуемся т.Пифагора.
по т. Пифагора:ВС= \sqrt{ AB^{2} - AC^{2} }= \sqrt{ 8^{2} - 4^{2} }= \sqrt{64-16} = \sqrt{48} [/tex]
ОТВЕТ : корень квадратный из 48