Объяснение:
Клумба - це фігурна квіткова ділянка у формі геометричної фігури (круга, овала, квадрата, трикутника, прямокутника) або зірчаста, діаметром від 0,75 м до 6 м і більше. Поверхня її завжди трохи опукла з ухилом, а рослини на клумбі саджають так, щоб вони утворювали візерунок або малюнок. Такі квітники слугують як місця для відпочинку та окраси. Одна сторона клумби трикутної форми дорівнює 2 м, друга - на 1/7 м менша від першої, а третя - на 5/7 менша від першої сторони. 1) Яка довжина невідомих сторін клумби? 2) Знайдіть периметр клумб. 3) Скільки коштуватиме огородження всієї клумби самшитом, якщо ціна 1 саджанця - 50 грн, а висаджують їх на відстані 25 см один від одного?
Умова:
Відповідь:
Одна - 2 м
Друга - ? м, на 1/7 менша першої
Третя - ? м, на 5/7 менша першої
1) 14/7 - 1/7 = 13/7 = 1 6/7 (м) - друга;
2) 14/7 - 5/7 = 9/7 = 1 2/7 (м) - третя;
3) 14/7 + 13/7 + 9/7 = 36/7 = 5 1/7 (м) - периметр;
4) 4 • 5 • 50 = 1000 (грн) - треба для огородження клумби садженцями.
Глобус, так же как и Земля, имеет форму шара. Следовательно, он даёт нам правильное представление о форме нашей планеты.
И глобус, и Земля вращаются вокруг собственной оси. При этом ось глобуса имеет такой же наклон, как и земная. Таким образом, глобус позволяет нам наблюдать этот вид движения Земли.
Глобус даёт правильное представление о форме, размерах, взаимном расположении крупнейших географических объектов: материков и островов, океанов, морей и рек.
Глобус модель Земли.png
Но так как глобус намного меньше Земли, на нём невозможно показать какую-либо местность подробно. Его неудобно использовать и во время путешествий.
Объяснение:
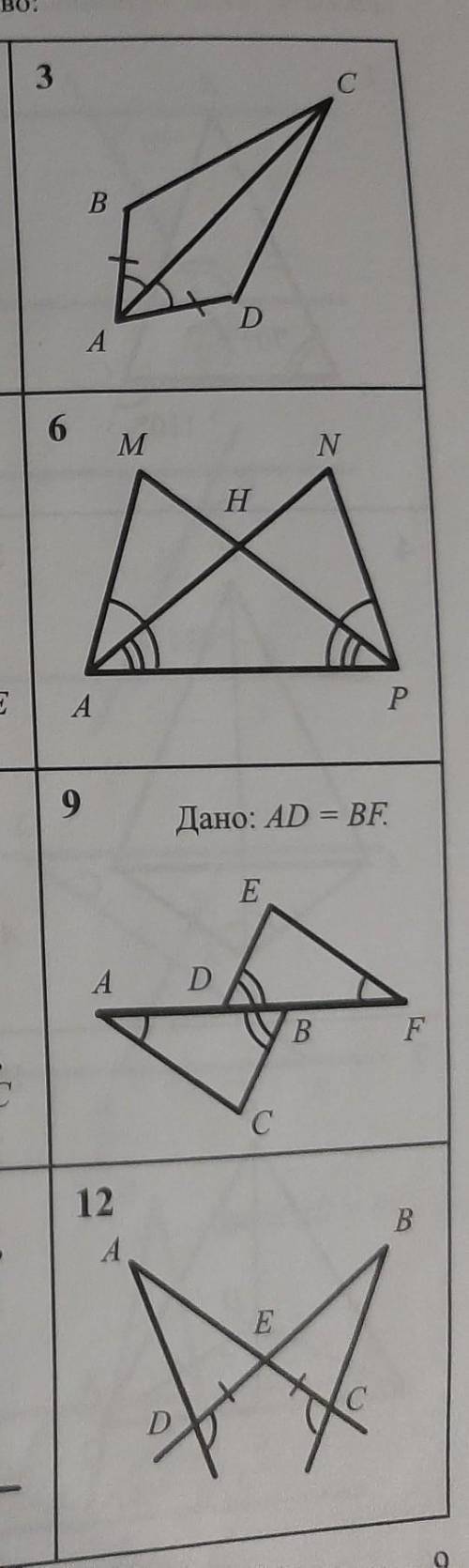
3. АВ = AD по условию,
∠ВАС = ∠DAC по условию,
АС - общая сторона для треугольников ВАС и DAC, ⇒
ΔВАС = ΔDAC по двум сторонам и углу между ними.
6.
а) ∠МАВ = ∠NBA по условию,
∠МВА = ∠NAB по условию,
АВ - общая сторона для треугольников МАВ и NBA, ⇒
ΔМАВ = ΔNBA по стороне и двум прилежащим к ней углам.
б) АМ = BN из равенства ΔМАВ = ΔNBA (см. п. а))
∠АМН = ∠ВNН из равенства ΔМАВ = ΔNBA,
∠МАН = ∠МАВ - ∠НАВ
∠NBH = ∠NBA - ∠HBA, а так как ∠МАВ = ∠NBA по условию и ∠НВА = ∠НAB по условию, то и
∠MAH = ∠NBH, ⇒
ΔMAH = ΔNBH по стороне и двум прилежащим к ней углам.
9. ∠САВ = ∠EFD по условию,
∠АВС = ∠EDF по условию,
АВ = AD + DB
FD = FB + DB, а так как AD = BF по условию, то и
АВ = FD, ⇒
ΔСАВ = ΔEFD по стороне и двум прилежащим к ней углам.
12. DE = CE по условию,
∠ADE = ∠BCE как смежные с равными углами,
∠AED = ∠BEC как вертикальные, ⇒
ΔAED = ΔBEC по стороне и двум прилежащим к ней углам.