См. Объяснение
Объяснение:
№ 1.
Считаем количество клеток до линии ВС - 4 клетки.
В условии сказано, что размер одной клетки 1 х 1, но при этом не сказано, чего (миллиметров, сантиметров, метров и т.д.). Поэтому и ответ надо дать в виде безразмерной величины.
ответ: 4.
№ 2.
Рассчитаем расстояния между точками.
Согласно теореме Пифагора:
АС = √(1² + 2²) = √5, где 1 и 2 - количество клеток по горизонтали и по вертикали.
АВ = √(2² + 1²) = √5, где 2 и 1 - количество клеток по горизонтали и по вертикали.
ВС = √(1² + 3²) = √10, где 1 и 3 - количество клеток по горизонтали и по вертикали.
Так как АС = АВ = √5, то треугольник АВС - равнобедренный.
А т.к. ВС² = АС² + АВ² = √((√5)² +(√5)²) = √10, то треугольник АВС - прямоугольный.
В равнобедренном треугольнике углы при основании равны.
Следовательно, угол АВС равен углу АСВ и равен:
∠АВС = (180°-90°) : 2 = 45°
ответ: ∠АВС = 45°
S = 675√3 см².
Объяснение:
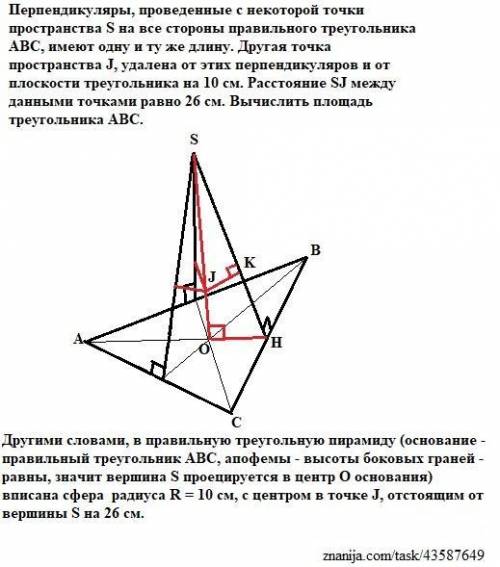
Задача: Перпендикуляры, проведенные с некоторой точки пространства S на все стороны правильного треугольника ABC, имеют одну и ту же длину. Другая точка пространства J, удалена от этих перпендикуляров и от плоскости треугольника на 10 см. Расстояние SJ между данными точками равно 26 см. Вычислить площадь треугольника.
Другими словами, в правильную треугольную пирамиду (основание - правильный треугольник АВС, апофемы - высоты боковых граней - равны, значит вершина S проецируется в центр О основания) вписана сфера радиуса R = 10 cм, с центром в точке J, отстоящим от вершины S на 26 см.
В прямоугольном треугольнике SKJ по Пифагору найдем катет SK = √(SJ²-JK²) = √(26²-10²) = 24 см.
Прямоугольные треугольники SKJ и SOH подобны по острому углу OSH - общий. SO = SJ + JO = 26+10 = 36 см. Из подобия имеем:
SO/SK = OH/JK.
OH = JK·SO/SK = 10·36/24 = 15 см.
Отметим, что ОН = (1/3)·АН так как точка О - центр правильного треугольника, точка пересечения его высот и медиан. Тогда АН = 15·3 = 45 см. Это высота треугольника АВС.
Тогда по известной формуле h = (√3/2)·a находим сторону треугольника.
а = 45·2/√3 = 30√3 см.
Площадь правильного треугольника равна S = (√3/4)·a².
S = (√3/4)·(30√3)² = 2700·√3/4 = 675√3 см².
Умоляю, поверьте, задача легкая.)
1.Рисунок очень простой. Пересекаем два отрезка под углом 90 градусов. Сможете нарисовать? Два треугольника АДО и ОСВ, в них угол АДО оказывается равным углу ОСВ, но это внутренние накрест лежащие при прямых АД И ВС и секущей АВ, значит, по признаку параллельности прямых прямые параллельны.
2. В треугольнике СС₁В СВ- гипотенуза, а высота СС₁- катет, лежащий против угла В, значит, угол В равен 30° по свойству, а в треугольнике АВС угол А тогда равен 180°-90°-30°=60°
Сожалею, нет такой возможности, нарисовать рисунок. Старенький икс пи..
Третий не строю, по той же причине. Но аналитически расскажу.
Сначала строите основание. потом делите его пополам и из середины прововдите высоту, т.к. ею будет Ваша медиана, т.к. проводили Вы ее к основанию в равнобедренном треугольнике. СОединяете теперь концы основания с полученной точкой - вторым концом медианы. Все. Задача закончилась. Успехов!