так как треугольник равносторонний, то все медианы являются и биссектрисами и высотами, тоесть медианы делят треугольник на 6 маелньких, каждый из которых прямоугольный (из-за высот) и один из его углом равен 30 градусам (из-за биссектрис, так как они делят углы основного треугольника пополам, а мы знаем, что все глы равностороннего трегольника по 60 градусов) отсюда ещё один угол, каждого из 6 треугольников ( а это и есть углы пересечения медиан) равен 180-90-30=60 градусов
Форму земной поверхности,все её возвышения и понижения называют рельефом местности в одних местах не видно ни возвышенностей,ни понижения.Такая местность называется равниной.Есть равнины с поверхностью ровной,как стол.Их называют плоскими равнинами.На карте они отмечены зелёным цветом.Некоторые равнины занимают пониженные участки.Они отмечаются на карте тёмно-зелёным цветом.Есть равнины,на которых выделяются холмы.Это холмистые равнины.На карте они отмечаются жёлтым или светло-коричневым цветом.
Объяснение:
Дано ∆АВС, <С=90
<(СЕ)(АВ)=90
Р(АЕС)=12,. Р(ВЕС)=5
Р(АВС)
Решение.
Р(АВС)=АВ+АС+ВС
Р(АЕС)=АС+АЕ+СЕ)=12
Р(ВЕС)=ВС+ВЕ+СЕ)=5
Для решения системы уравнений вычтим и сложим обе части между собой
Р(АВС)=АВ+АС+ВС;. АВ=АЕ+ЕВ,
12+5=АС+АЕ+СЕ+ВС+ВЕ+СЕ
17= Р(АВС)+2СЕ
12-5=АС+АЕ+СЕ- ВС -ВЕ -СЕ
7 = АС+АЕ -ВС -ВЕ
Воспользуемся свойством высоты прямоугольного треугольника h^2=AE*EB,
AC^2=AE^2+CE^2
BC^2=BE^2+CE^2. вычтим из
АС^2 -BC^2=AE^2 -BE^2
AC^2 + BC^2 = AE^2+2CE^2+BE^2
AB^2=(AE+BE)^2=AE^2+2AE*BE+BE^2
вычтим/сложим одно из/с другого,
2СЕ^2 - 2АЕ*ВЕ;
. СЕ^2=АЕ*ВЕ. CE=AC*BC/AB
2АВ^2=2AE
P(ABC)=17 - 2√(AE*BE)
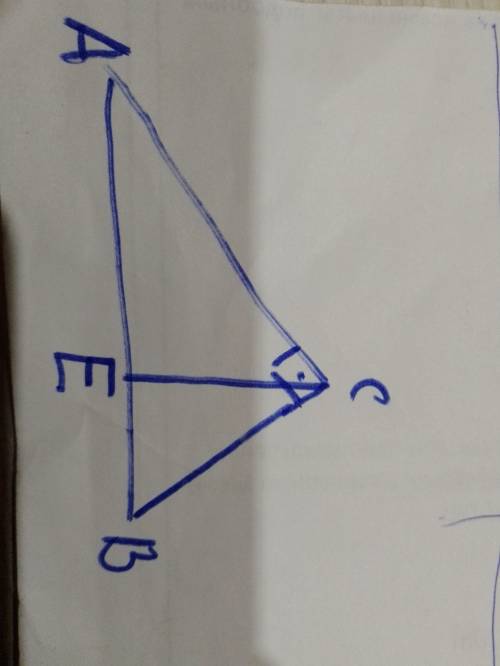
равносторонний треугольник
стороны равны - обозначим k
по теореме косинусов для любого теугольника
a^2 = b^2 +c^2 - 2 bc * cosA <все стороны k
k^2 = k^2 +k^2 -2k^2 *cos A
k^2 = 2k^2 -2k^2 *cos A
k^2 = 2k^2 (1-cos A)
1/2 = 1-cos A
cosA = 1-1/2 =1/2 =cos60
<A = 60 град <это верно для всех трех углов
рещено наверно правильно