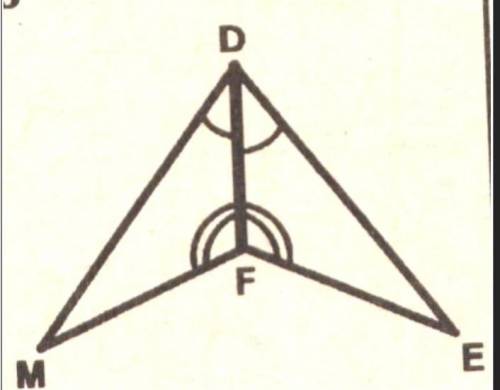
1) ∠MDF = ∠FDE - по условию
2) ∠DFM = ∠DFE - по условию
3) DF - общая сторона
следовательно треугольники MDF и DFE равны по стороне и двум прилежащим к ней углам
ответ: (sin^2t-1)/(cos^2t-1) + tgt•ctgt=
=(sin^2t-sin^2t-cos^2t)/(cos^2t-sin^2t-cos^2t)+1=
=(-cos^2t/-sin^2t) +1=(cos^2t/sin^2t)+1=(cos^2t+sin^2t)/sin^2t=1/sin^2t. Это первое)
2 не смогла).
cos^2t-ctg^2t)/(sin^2t-tg^2t)
cos^2t-ctg^2t=cos^2t-cos^2t/sin^2t=(cos^2t*sin^2t-cos^2t)/sin^2t=
=(-cos^2t(1-sin^2t))/sin^2t=-cos^4t/sin^2t
sin^2t-tg^2t=sin^2t-sin^2t/cos^2t=(sin^2t*cos^2t-sin^2t)/cos^2t=
=(-sin^2t(1-cos^2t))/cos^2t=-sin^4t/cos^2t
-cos^4t/sin^2t:(-sin^4t/cos^2t)=cos^6t/sin^6t=ctg^6t. Это третье).
Объяснение:
угол A равен углу А1, АВ равно А1В1, АС равно А1С1. Докажем, что треугольники равны. Наложим треугольник ABC на треугольник A1B1C1 так, чтобы угол A совместился с углом A1. Так как АВ=А1В1, а АС=А1С1, то B совпадёт с В1, а C совпадёт с С1.Значит, треугольник А1В1С1 совпадает с треугольником АВС, а следовательно, равен треугольнику АВС. 2) Луч С1С совпадает с одной из сторон этого угла. A лежит на CC1. AC=A1C1, BC=B1C1, ∆C1BC – равнобедренный, ∠ACB=∠A1C1B1.
3) Луч C1C проходит вне угла А1С1В1. AC=A1C1, BC=B1C1, значит, ∠1 = ∠2, ∠1+∠3 = ∠2+∠4, ∠ACB=∠A1C1B1. Итак, AC=A1C1, BC=B1C1, ∠C=∠C1. Следовательно, треугольники ABC и A1B1C1 равны по первому признаку равенства треугольников.
сторона DF - общая, а прилежащие к ней углы - равны, т.е. этот треугольник равен по 2-му признаку. сторона и прилежащие к ней углы.