Несмотря на то, что прямоугольный треугольник, сторонами которого являются высота, медиана и отрезок гипотенузы между ними, является Пифагоровым (8, 15,17), и высота делит гипотенузу, длина которой равна 17*2 = 34, на отрезки длиной 17 - 8 = 9 и 17 + 8 = 25 (как и положено, 9*25 = 15^2), сам треугольник не является целочисленным, и его катеты надо просто вычислить по теореме Пифагора.
Меньший катет равен √(9^2 + 15^2) = 3*√34;
Больший катет равен √(25^2 + 15^2) = 5*√34;
Ну да, еще периметр 34 + 8*√34 ;
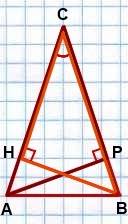
Рассмотрим треугольники ACP и BCH.
1) AC=BC (по условию (как боковые стороны равнобедренного треугольника))
2) ∠C — общий
∠APC=∠BHC=90º (так как AP и BH — высоты (по условию)).
Сумма углов треугольника равна 180º .
В треугольнике ACP
∠CAP=180º — (∠APC+∠C)=180º — 90º — ∠C=90º — ∠C.
В треугольнике BCH
∠CBH=180º — (∠BHC+∠C)=180º — 90º — ∠C=90º — ∠C.
Отсюда,
3) ∠CAP=∠CBH.
Следовательно, треугольники ACP и BCH равны
(по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: AP=BH.
Что и требовалось доказать.
ответ: я пишу потому что 20 символов нужно
Объяснение: