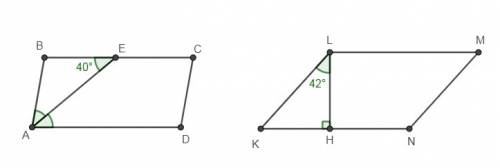
а) Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник ⇒ ∠ВАЕ = ∠ВЕА = 40°
∠А = 2∠ВАЕ = 2 * 40 = 80° (так как АЕ - биссектриса ∠А)
Сумма соседних углов параллелограмма равна 180° ⇒
∠В = 180 - ∠А = 180 - 80 = 100°
Противоположные углы параллелограмма равны ⇒
∠С = ∠А = 80°
∠D = ∠В = 100°
ответ: 80°; 80°; 100°; 100°.
-------------------------------------------------------------------------
б) ΔKLH - прямоугольный ⇒ ∠К = 90 - 42 = 48°
Сумма соседних углов параллелограмма равна 180° ⇒
∠L = 180 - ∠K = 180 - 48 = 132°
Противоположные углы параллелограмма равны ⇒
∠M = ∠K = 48°
∠N = ∠L = 132°
ответ: 48°; 48°; 132°; 132°.
Углы при основании равнобедренного треугольника равны. Если этот угол равен 60°, значит и угол при вершине равен 60° (сумма внутренних углов треугольника равна 180°, 180°-120°=60°). Значит треугольник РАВНОСТОРОННИЙ (правильный). Высота правильного треугольника является и его медианой, и его биссектрисой. Пусть половина стороны равна х, тогда сторона равна 2х (так как катет х лежит против угла 30°). По Пифагору 4х² =(√3)²+х². => х=1. Итак, сторона треугольника равна 2.
ответ: стороны треугольника равны 2см.
Есть у нас трапеция АВСD. У нее есть высоты BH1 и CH2, и диагональ АС.
1. Поскольку высоты BH1 и CH2 параллельны, отрезок Н1Н2 = ВС.
2. Поскольку трапеция равнобедренна, то АН1 = DH2
3. Полусумма оснований (АD + BC)/2 = (АН1 + H1H2 + H2D + ВС)/2 = (2 * АH1 + 2 * H1H2) /2 = АH1 + H1H2 = АH2.
4. Треугольник АСН2 - прямоугольный, поскольку СН2 перпендикулярна к АН2. Из теоремы Пифагора АH2 = √(АС² - CH2²) = 8.
5. Площадь равна произведению высоты на полусумму оснований S = АH2 * CH2 = 8 * 6 = 48