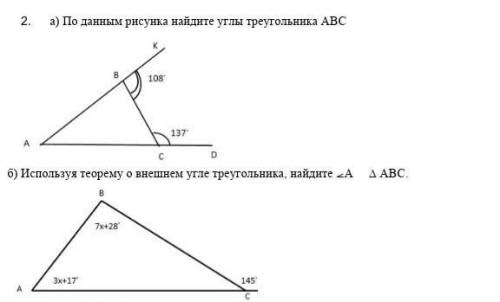
Внутренний угол треугольника и смежный ему внешний в сумме равны 180 градусов
<В=180-108=72 градуса
<С=180-137=43 градуса
Сумма всех углов треугольника равна 180 градусов
<А=180-(72+43)=65 градусов
Номер 2
Сумма двух внутренних углов не смежных с внешним углом равна градусной мере внешнего угла
7Х+28+3Х+17=145
10Х+45=145
10Х=145-45
10Х=100
Х=100:10
Х=10
<В=7•10+28=98 градусов
<А=3•10+17=47 градусов
Объяснение:
Обозначим прямоугольник ABCD и точку пересечения диагоналей O как
B C
E O
A D
Треугольник AOB равнобедренный, поэтому высота OE является и медианой. Тогда, так как AB=14, AE=7. По теореме Пифагора из прямоугольного треугольника AEO находим AO^2=EO^2+AE^2=49+36=85. AO=sqrt(85). Тогда AC=2sqrt(85) и AC^2=4*85=340. Из прямоугольного треугольника ABC по теореме Пифагора BC^2=AC^2-AB^2=340-196=144. Значит BC=12. Тогда площадь прямоугольника равна AB*BC=14*12=168.
ответ:168.
1. Значения синуса, косинуса и тангенса на рисунке.
2. Тригонометрические тождества
sin²α + cos²α = 1 - основное тригометрическое тождество
tgα*ctgα = 1
формулы приведения:
sin(90-a)=cosa, cos(90-a)=sina - формулы приведения для острого угла
sin(180-a)=sina, cos(180-a)=cosa - формулы приведения для тупого угла
3. Теорема косинусов:
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a²=b² + c² - 2bc cosα
4. Теорема синусов:
Стороны треугольника пропорциональны синусам противолежащих углов.
a/sinA = b/sinB = c/sinC
5. Расстояние между двумя точками:
Пусть А и B - две точки в плоскости. Их координаты соответственно равны A(x₁;y₁), B(x₂;y₂). Тогда расстояние между ними равно
AB = √(x₂-x₁)² + (y₂-y₁)² (корень из всего выражения)
6. Координаты середины отрезка:
Середина отрезка AB на плоскости с концами в точках A(Xa;Ya) и B(Xb;Yb) имеет координаты
AB = ( (Xa + Xb)/2 ; (Ya + Yb)/2)
7. Радиус описанной окружности вокруг треугольника находится по формуле:
R = abc/4S или R = a/2 sinα , где
R - радиус окружности,
a,b,c - стороны треугольника,
S - площадь треугольника,
α - угол, лежащий напротив стороны a
8. Формулы площади треугольника - (см. рисунок).
9. Формулы нахождения площади четырёхугольника:
Площадь прямоугольника:
S = ab
Площадь квадрата:
10. Правильный многоугоольник — это выпуклый четырёхугольник, у которого все стороны и углы равны.
11. Длину дуги окружности:
L = πrα/180⁰
Длину окружности с радиусом можно вычислить по формуле
L = 2πr
12. Прямоугольная система координат на плоскости (см. рисунок).
13. Уравнение окружности:
В прямоугольной системе координат уравнение окружности радиуса r с центром в точке C (x₀;y₀) имеет вид:
(x-x₀)² + (y-y₀)² = R²
14. Уравнение прямой:
имеет вид:
ax + by + c =0, ult
x, y - координаты точки;
a,b,c - некоторые числа.
С тебя синус,косинус и тангенс углов от 0 градус до 180 градусов . 2)тригонометрическое тождества. 4) тео">
а) Дано: ∆ АВС , /_ КВС= 108°, /_ BCD= 137°
Найти: /_ АВС, /_ ВАС, /_ ВСА
1) /_ АВС= 180° -108° = 72°
2) /_ ВСА= 180° - 137°= 43°
3) /_ ВАС= 180°- (72°+43°) = 180°- 115°= 65°
ответ: /_ АВС= 72° , /_ ВСА= 43°, /_ ВАС= 65°.
б) Дано: ∆ АВС, /_ А= 3х+17, /_ В= 7х+28, /_ С ( внешний) = 145°
Найти: /_ А
1) /_А+/_В=/_ С (внеш.)
составим уравнение:
2) /_ А= 3х+17
/_ А= 3•10+17=30+17=47°
ответ: /_ А= 47°