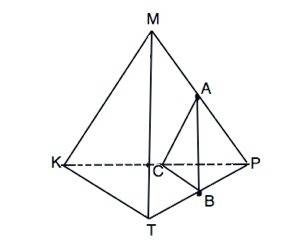
По условию секущая плоскость параллельна плоскости КМТ.
Точки А и В лежат в плоскости грани МРТ и являются серединами сторон МР и ТР треугольника МТР.
Следваоетльно, прямая АВ параллельна МТ.
Из т.В проведем прямую ВС параллельно КТ.
ВС - средняя линия ∆ КТР.
С- середина КР, АС - средняя линия ∆ МКР и параллельна МК.
Две пересекающиеся прямые АВ и МС плоскости АВС параллельны двум пересекающимся прямым МТ и ТК плоскости МКТ. Это признак параллельности плоскостей, следовательно, АВС - искомое сечение.
1) Угол А = S углов треугольника - (угол С + угол В) = 180 - (45+30) = 105 градусов. (S углов треугольника априори равна 180 градусов.)
2) Используем теорему синусов, которая гласит, что А/sinA = B/sinB или A/sinA = C/sinC.
Отсюда угол В:
5/sin105 = x/sin30
5/0.9659258263 = х/0,5
x = (5 * 0,5)/0.9659258263 = 2,41481456575 см
Угол С:
5/sin105 = x/sin45
5/0.9659258263 =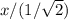
x = 5 * 1/(корень из 2)/0.9659258263 = 3,660254037872597 см.
ответ: Угол А = 105 градусов; В = 2,41 см; С = 3,66 см.