
2
Объяснение:
Найдем сначала x. Пусть окружность касается AB и BC в точках K и L соответственно. Тогда BK=BL=x. Аналогично CL=x. Тогда BC=2x => x=1. Радиус, проведенный в точку касания, перпендикулярен к касательной. Тогда, если O - центр окружности, OK=OL=R и OK⊥AB, а OL⊥BC. Значит ∠KBL+∠KOL=180°. Тогда по теореме косинусов для четырехугольника KBLO можно выразить KL² двумя через OK=OL=R и BK=BL=1. Приравняем KL². Получим: 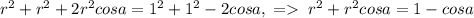 . Здесь cosa - косинус ∠KBL.
. Здесь cosa - косинус ∠KBL. 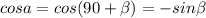 , где
, где 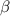 - угол ABH. AB=10x=10, а AH=(14-2)/2=6 =>
- угол ABH. AB=10x=10, а AH=(14-2)/2=6 => 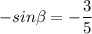 . Подставим это:
. Подставим это: 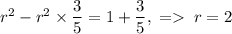 .
.
Задание выполнено!
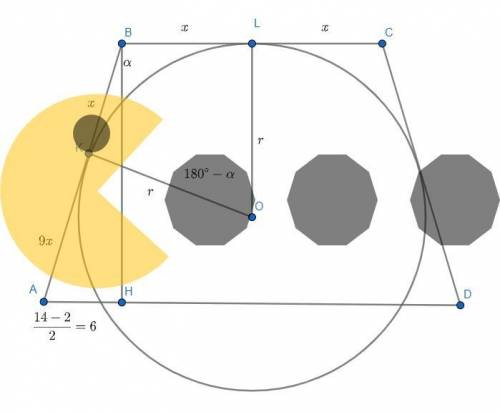
Дано :
Четырёхугольник ABCD — трапеция (AB || CD).
AB : CD = 3 : 5.
Отрезки BD и AC — диагонали.
Точка О — точка пересечения диагоналей.
S(∆COD) = 50 (ед²).
Найти :
S(∆AOB) = ?
Диагонали трапеции, пересекаясь, образовывают два подобных треугольника (подобны только те, одни из сторон которые являются основания трапеции).Отсюда —
∆DOC ~ ∆ВОА.
<DOC = <BOA (как вертикальные).
Тогда AB и CD — сходственные стороны (по определению).
Отношение сходственных сторон подобных треугольников равно коэффициенту подобия.Пусть AB = 3x, тогда CD = 5x (по условию задачи).
Тогда —
k = AB/CD = 3x/5x = 3/5 = 0,6.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.Отсюда —
S(∆BOA)/S(∆DOC) = k² (здесь главное написать всё в том порядке, в котором мы делали. То есть, ища коэффициент подобия, мы ставили в числитель меньший треугольник, так и здесь : в числитель ставим меньший треугольник).
S(∆BOA)/50 (ед²) = 0,6²
S(∆BOA)/50 (ед²) = 0,36
S(∆BOA) = 18 (ед²).
18 (ед²).
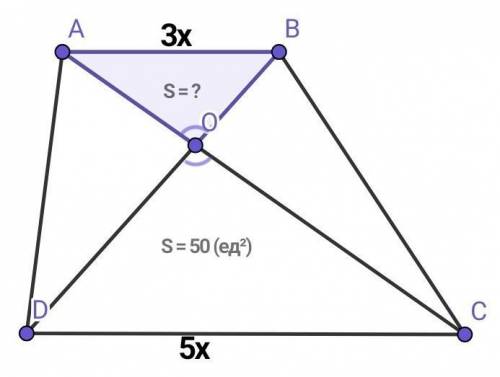
На рисунке изображена прямоугольная трапеция ABCD, в которую вписан круг. Точка касания окружности делит большую боковую сторону на отрезки длиной 4 см и 25 см. Установите соответствие между началом предложения (1 - 4) и его окончанием (а-д) так, чтобы образовалось правильное утверждение
1 Средняя линия трапеции равна ,2 Высота трапеции равна , 3 радиус вписанной окружности равен , 4 Меньшая диагональ трапеции равна
A )√ 594 см , Б) 20 см, В)2√149 см , Г) 10 см , Д) 24,5 см
Объяснение:
1) Найдем радиус вписанной окружности r=√(CH*HD)=√(4*25)10 (cм)⇒
диаметр ,равный высоте трапеции , равен 2*10=20( см), h=20 cм.
2)Высота прямоугольной трапеции равна меньшей боковой стороне ⇒ АВ=20 см.
3)Суммы противоположных сторон любого четырёхугольника описанного около окружности равны : АВ+CD=BC+AD ⇒BC+AD=20+29=49 (см)
По определению средней линии трапеции имеем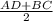 =
=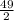 =24,5(см)
=24,5(см)
4) Меньшей диагональю будет АС.
По свойству отрезков касательных СН=СК=4 см, ВМ=ВК=10 см, тогда ВС=4+10=14 (см)
ΔАВС-прямоугольный по т. Пифагора АС=√(14²+20²)=√596=√(4*149)=2√149 ( см).
ответ . 1-Д ; 2-Б ; 3-Г ; 4-В .