
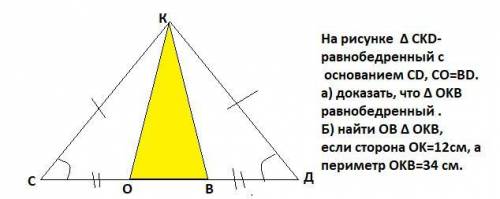
На рисунке Δ CKD-равнобедренный с основанием CD, CO=BD .
а) доказать, что Δ OKB равнобедренный ?
Б) найти OB Δ OKB, если сторона OK=12см, а периметр OKB=34 cм.
Объяснение:
1) Т.к. Δ СКД равнобедренный , то СК=ДК и углы при основании равны ∠С=∠Д.
2)ΔКСО=ΔКДС по 2 сторонам и углу между ними : СК=ДК п.1, ∠С=∠Д п.1, СО=ВД по условию.
В равных треугольниках соответственные элементы равны ⇒КО=КВ ⇒ΔОКВ-равнобедренный по определению.
3)Р(ОКВ)=ОВ+КО+КВ, 34=ОВ+12+12, поэтому ВО=10(см)
из вершины D опустим высоту DH на сторону BC. Точку пересечения диагоналей ромба обзовём К.
т.к в ромбе диагонали пересекаются под прямым углом и точкой пересечения делятся пополам, то СК = AC/2 = 16/2 = 8, BK =KD = BD/2 = 12/2 = 6
из прямоугольного треугольника BKC гипотенуза BC = sqrt(BK^2 + KC^2) = sqrt(8^2 + 6^2) = 10
площадь треугольника BCD, вычесленная как половина произведения стороны на высоту, опущенную на эту сторону
с одной стороны равна 1/2 * BD * CK
с другой стороны 1/2 BC * DH
отсюда DH = BD * CK / BC = 12 * 8 / 10 = 9.6
DH является расстоянием между прямыми MD и BC т.к перепендикулярен обеим прямым. Отсюда угол между BMC и BDC равен арктангенсу MD/DH = arctg(9.6 / 9.6) = 45 градусов
плоскость ABC и BDC - это одно и то же, т.к все точки ромба лежат в одной плоскости. Поэтому искомый угол равен 45 градусам
1. В основании – прямоугольник, поэтому треугольник ABD – прямоугольный. По теореме Пифагора находится его гипотенуза.
BD−→−=AB2+AD2−−−−−−−−−−√=62+82−−−−−−√=10
2. Достроим четырехугольник KPRM, где P и R – середины BB1 и DD1 соответственно.
По признаку параллелограмма все четыре получившихся четырехугольника ABPK,BCMP,CMRD и AKRD – параллелограммы.
Следовательно, KPRM – тоже параллелограмм, причем равный основаниям параллелепипеда. А значит, и прямоугольник.
Диагонали прямоугольника KM=PR=BD= равны. Следовательно, KM−→−=10
3. Рассмотрим прямоугольный треугольник CC1L. Угол CC1L равен углу B1BC, который в свою очередь равен 60° по условию. Следовательно, угол C1CL=30°. По теореме о катете напротив угла в 30° гипотенуза CC1=2⋅LC1=2⋅4=8.
И CC1−→−=8
4. Рассмотрим треугольник B1CC1.
Его уголCC1B1=60° , его стороны CC1 и B1C1
Объяснение:
во втором 10
Объяснение: