Теорема
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Доказательство. Пусть у треугольников ABC и A1B1C1 ∠ A = ∠ A1, AB = A1B1, AC = A1C1.
Пусть есть треугольник A1B2C2 – треугольник равный треугольнику ABC, с вершиной B2, лежащей на луче A1B1, и вершиной С2 в той же полуплоскости относительно прямой A1B1, где лежит вершина С1.
Так как A1B1=A1B2, то вершины B1 и B2 совпадают.
Так как ∠ B1A1C1 = ∠ B2A1C2, то луч A1C1 совпадает с лучом A1C2.
Так как A1C1 = A1C2, то точка С1 совпадает с точкой С2. Следовательно, треугольник A1B1C1 совпадает с треугольником A1B2C2, а значит, равен треугольнику ABC. Теорема доказана.
Правильный четырехугольник - это квадрат.
Радиус вписанной в него окружности равен половине стороны. ⇒
а=2r
P=4•2r=8r
C=2πr
P/C=8r/2πr=4/π, и это величина для квадрата постоянная.
По данным задачи:
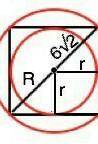
Радиус окружности, описанной около квадрата, равен половине диагонали квадрата.
Тогда диагональ квадрата 2•R=12√2
Сторона квадрата – катет равнобедренного прямоугольного треугольника с гипотенузой 12√2 и острыми углами 45°
а=12√2•sin45°=6√2•√2:2=12
Р=4•12=48
Радиус вписанной окружности r=12:2=6
С=2•p•6=12π
Как найти площадь
Определения
Площадь является одним из основных математических понятий. Она характеризует как плоские, так и поверхностные геометрические объекты.
Площадью плоской замкнутой фигуры называется величина части плоскости, которая находится внутри указанной фигуры.
Единицей измерения площади плоской фигуры является квадрат со стороной, равной единице. Число, соответствующее площади некоторой фигуры, состоящей из частей, равно сумме чисел, соответствующих площадям этих частей. Измерение площадей треугольников и многоугольников основано на возможности построения равновеликих им прямоугольников.
Площадь произвольной ограниченной плоской фигуры определяется как общий предел площадей описанных и вписанных в нее многоугольников, наибольшие стороны которых по длине стремятся к нулю.
Если фигура имеет площадь, то она называется квадрируемой.
Формулы площади основных геометрических фигур
Площадь треугольника
Чтобы найти площадь треугольника, надо найти полупроизведение двух его сторон на синус угла между ними. То есть если известны длины двух сторон треугольника , которые равны  и , а также угол  между этими сторонами, то искомая площадь:


Читать дальше: формулы площади треугольника и примеры решений →
Площадь круга
Чтобы найти площадь круга, надо найти произведение числа  на квадрат радиуса этого круга, то есть


Читать дальше: формула площади круга и примеры решений →
Площадь квадрата
Чтобы найти площадь квадрата, надо длину его стороны возвести в квадрат, то есть


Читать дальше: формула площади квадрата и примеры решений →
Площадь прямоугольника
Чтобы найти площадь прямоугольника, надо его длину умножить на ширину, то есть


Читать дальше: формула площади прямоугольника и примеры решений →
Площадь параллелограмма
Чтобы найти площадь параллелограмма, нужно найти произведение стороны  параллелограмма на высоту , проведенную к этой стороне, то есть


Если 2 стороны и угол между ними одного треугольника соответственно равны 2-м сторонам и углу между ними другого треугольника, то такие треугольники равны.
Докозательство:
Рассмотрим треугольники АВС и KLM, у которых AB=KL, AC=KM, и угол A= углу К.
Т.к угол A= углу К, то треугольник АВС можно наложить на треугольник KLM так, что вершина А совместиться с вершиной Л, а стороны АВ и АС наложатся соответственно на стороны KL и KМ.
Поскольку AB=KL, AC=KM, то соответственно равные стороны наложатся друг на друга, следовательно, совместятся стороны BC и LM.
Т.к. треугольники полностью совместятся, следовательно, они равны.
Из учебника геометрии 7-9 класс.