Дано: прямоугольный треугольник АВС;
угол С = 90;
СА = 3;
СВ = 4;
СН - высота.
Найти: СН - ?
1) рассмотрим прямоугольный треугольник АВС. Тогда по теореме Пифагора:
АС^2 + СВ^2 = АВ^2;
3^2 + 4^2 = АВ^2;
9 + 16 = АВ^2;
25 = АВ^2;
АВ = 5;
2) В прямоугольном треугольнике каждый катет - это среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу. Тогда
ВС = √( АВ * НВ);
4 = √( 5 * НВ) (возведем правую и левую часть в квадрат);
16 = 5 * НВ;
НВ = 16/5;
НВ = 3,2;
3) АС = √( АВ * НА);
3 = √( 5 * НА) (возведем правую и левую часть в квадрат);
9 = 5 * НА;
НА = 9/5;
НА = 1,8;
4) СН = √АН * НВ;
СН = √1,8 * 3,2;
СН = √5,76;
СН = 2,4.
ответ: 2,4.
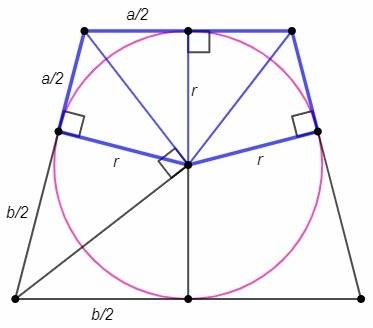
Около трапеции описана окружность, следовательно трапеция равнобедренная (т.к. сумма противолежащих углов равна 180). Биссектрисы углов при основании образуют равнобедренный треугольник (половины равных углов равны). Радиус вписанной окружности делит основание пополам (т.к. является высотой и медианой). Отрезки касательных, проведенных из одной точки, равны. Таким образом, искомый пятиугольник разделен на четыре равных (по двум катетам) прямоугольных треугольника.
S= 4*(a/2)r/2 =ar
Биссектрисы углов при боковой стороне перпендикулярны (т.к. сумма односторонних углов при параллельных равна 180). Радиус к боковой стороне является высотой из прямого угла и равен среднему пропорциональному проекций катетов.
r= √(a/2*b/2) =√(ab)/2
S= a√(ab)/2 =3√15/2
ответ:они равны по второму признаку
Объяснение:но это не точно посмотри на фотке