Задача №11
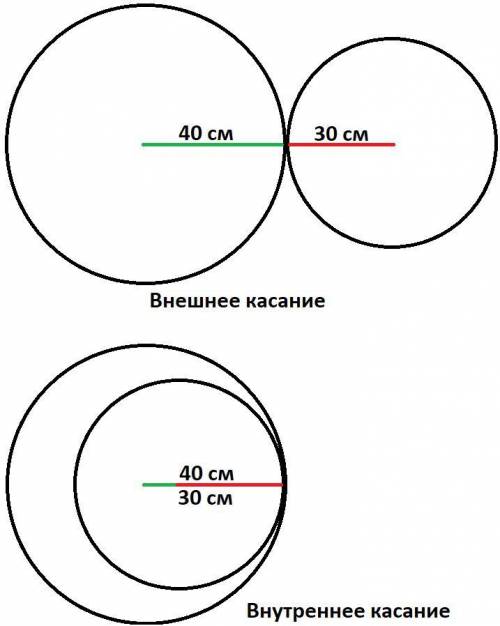
При внешнем касании расстояние между центрами будет равно сумме радиусов: 40 см + 30 см = 70 см.
При внутреннем касании расстояние между центрами будет равно разнице радиусов: 40 см - 30 см = 10 см.
ответ: при внешнем касании 70 см, при внутреннем касании 10 см.
Задача №12
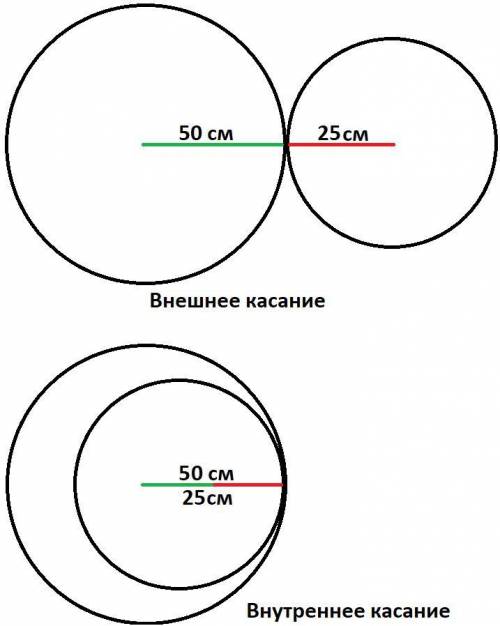
При внешнем касании расстояние между центрами будет равно сумме радиусов: 50 см + 25 см = 75 см.
При внутреннем касании расстояние между центрами будет равно разнице радиусов: 50 см - 25 см = 25 см.
Для внутреннего касания расстояние между центрами слишком большое, а для внешнего касания слишком короткое (не хватает 15 см).
Вывод: окружности с данными параметрами касаться не могут.
В основании квадрат. Радиус вписанной окружности = a/2
Апофему m можно найти по теореме Пифагора: m = sqrt(h^2+a^2/4)
Площадь боковой поверхности = 4 * площадь боковой грани = 4 * (0.5 * m * a) = 2a*sqrt(h^2+a^2/4)