1 Треугольник АВС, АВ=ВС=10, АС=12, ВН-высота= медиана, АН=НС=1/2АС=12/2=6, треугольник АВН прямоугольный, ВН=корень(АВ в квадрате-АН в квадрате)=корень(100-36)=8, площадьАВС=1/2АС*ВН=1/2*12*8=48
2. площадь параллелограмма=сторона1*сторона2*sin150=12*16*1/2=96
3. трапеция АВСД, АВ=СД=13, уголА=уголдД, ВС=10, АД=20, проводим высоты ВН и СК на АД, НВСК-прямоугольник, ВС=НК=10, треугольник АВН=треугольник КСД по гипотенузе и острому углу, АН=КД=(АД-НК)/2=(20-10)/2=5, ВН-высота трапеции=корень(АВ в квадрате-АН в квадрате)=корень(169-25)=12, площадьАВСД=1/2(ВС+АД)*ВН=1/2*(10+20)*12=180
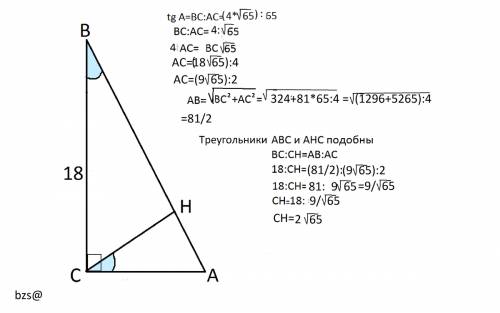
ответ: пусть т.О - пересечение диоганалей ромба ABCD: BD ⋂ AC = O, уго ODC = 60(по условию), рассмотрим треугольник DOC - прямоугольный, значит, исходя из определения косинуса, и свойства диоганалей ромба:
1)BD = OB+OD, OB=OD, значит OD = 4.
cos60=OD=DC
1/2=4/DC
DC=4/1/2=8