180-120=60 - сумма оставшихся углов
Т.к. тр. равнобедренный углы при основании равны, следовательно каждый угол 60\2=30
Высота проведённая в равнобедренном тр. является и медианой и биссектрисой,
следовательно делит основание пополам.
Рассмотрим образовавшийся прямоуг. тр.: По 2 свойству прямоуг. тр.: против угла в 30 градусов лежит катет равный половине гипотинузы. Тогда пусть катет лежащий против угла в 30 градусов будет A, тогда гипотинуза будет 2A.
По т. Пифагора (2A)²=A²+2²
A=√4/3
ответ: √4/3
Объяснение:
Условие задачи составлено некорректно. ——
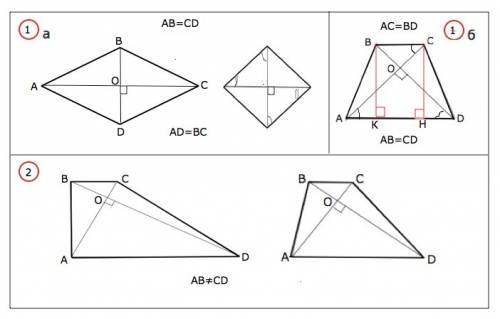
Данному в вопросе условию соответствуют четырехугольники на рисунке 2 вложения, равенство боковых сторон которых по данному условию доказать нельзя. Возможные варианты полного условия задачи:
а) Для равенства второй пары сторон должно быть дано равенство параллельных сторон: В четырехугольнике две стороны параллельны и равны, а диагонали взаимно перпендикулярны. Докажите, что две другие стороны равны между собой.
Сторона АВ равна и параллельна СD. Прямоугольные треугольники АОВ и СОD равны по гипотенузе и острым ( накрестлежащим) углам. Тогда равны и треугольники ВОС и АОD по двум катетам. Отсюда следует равенство АD=ВС. Следовательно, данный четырехугольник ромб или, как частный случай ромба, квадрат.
б) В четырехугольнике две стороны параллельны, а диагонали равны и взаимно перпендикулярны. Докажите, что две другие стороны равны между собой.
Здесь для доказательства равенства второй пары сторон перпендикулярность диагоналей не имеет значения. (см. рисунок). Доказывается через равенство площадей треугольников ВАD и СDA ( их высоты равны, BD=AC, АD- общая). Как следствие из Теоремы об отношении площадей треугольника острые углы между равными сторонами равны, из чего следует равенство ∆ ABD=∆ ACD и АВ=CD.
в) В четырехугольнике две стороны параллельны друг другу, а две другие перпендикулярны диагоналям. Докажите, что перпендикулярные диагоналям стороны равны между собой. (Решение есть на , повторять его здесь нет необходимости.)
я не знаю ну ща скажу подожди