ответ:8см
Объяснение:
За теоремой косинусов,
AB^2=AO^2+BO^2-2×AO×BO×cos/_AOB
AB^2=64+64-2×8×8×cos60°
AB^2=128-128×0.5
AB^2=64
AB>0, AB=8см.
^^^Это как один из вариантов решения. Можно не использовать теоремы косинусов, а действовать вот так: сначала доказать, что треугольник, так как две из его сторон равны(радиусы), он является равнобедренным т реугольником, а значит углы при основе равны. Угол при вершине известен, сума углов треугольника=180°, отсюда
2х+60=180
2х=120
х=60, а это значит что все углы треугольника=60°, а значит он равносторонний. Отсюда AO=OB=r(радиус)=AB=8см. Извиняюсь за слишком краткое описание второго метода, но первый более практичный))
Решение и подробное объяснение:
1) Стороны AB и AC правильного треугольника ABC лежат в двух перпендикулярных плоскостях. Найти площадь треугольника ABC, если точки B и C удалены от прямой пересечений плоскостей на 3√2
Формула площади правильного треугольника
S=(а²√3):4
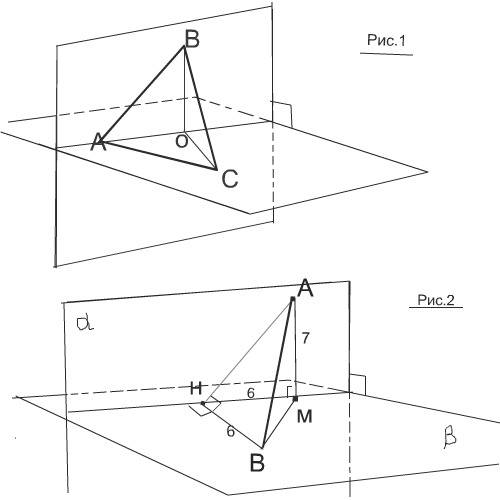
Рассмотрим рис.№1
Расстояние от В и С до прямой пересечений плоскостей - это проекции сторон АВ и АС на эту прямую.
Сторону треугольника найдем из равнобедренного прямоугольного треугольника ВОС
Пусть АВ=ВС=АС=а
а²=(ВО²+ОС²)=(3√2)²+(3√2)²=36
а=6
S=(а²√3):4=36√3):4=9√3
------------
2) Концы отрезка AB лежат в двух перпендикулярных плоскостях и удалены от прямой их пересечения на 6 и 7. Найти длину отрезка AB, если расстояние между основаниями перпендикуляров, проведенных из точек A и B к прямой пересечения, равны 6.
Рассмотрим рисунок №2.
АМ = расстояние от А до прямой пересечения плоскостей.
ВН - расстояние от В до прямой пересечения плоскостей.
Угол АНВ - прямой по теореме о трех перпендикулярах:
Если прямая (ВН), проведенная на плоскости через основание наклонной(АН), перпендикулярна её проекции (МН), то она перпендикулярна и наклонной.
В треугольнике АМВ отрезок АМ, лежащий в плоскости α, перпендикулярен линии пересечения плоскостей α и β, потому перпендикулярен ВМ, лежащему в плоскости β
ВН перпендикулярна НМ по условию ( расстояние от В до линии пересечения).
Найдем из треугольника ВМН сторону ВМ по тепореме Пифагора:
ВМ²=МН²+ВН²=72
Из треугольника АВМ найдем наклонную АВ:
АВ²=АМ²+ВМ²=49+72=121
АВ=√121=11
----------------
Можно АВ найти из треугольника АНВ:
АН=√(МН²+АМ²)=√(36+49)=√85
АВ=√(85+36)=√121=11
ответ:24 сантиметра
Объяснение: