
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.
Объяснение:
Рисунок прилагается.
Дано: ABC прямоугольный треугольник, ∠ С = 90°, CH- высота, AH = 2 см - проекция катета AC на гипотенузу, BH = 18 см - проекция катета BC на гипотенузу.
Найти катеты AC и BC.
Обозначим для удобства катеты AC = a, BC = b, проекции катетов AH = a₁, BH = b₁, высоту CH = h.
Высота в прямоугольном треугольнике, опущенная на гипотенузу, равна среднему пропорциональному проекций катетов на гипотенузу.
h² = a₁*b₁ = 2 * 18 = 36; h = 6
⇒ Высота треугольника, опущенная на гипотенузу CH = h = 6 см.
Из прямоугольного ΔACH по теореме Пифагора:
a² = h² + a₁² = 6² + 2² = 36 + 4 = 40; a = √40 = 2√10
Катет AC = 2√10 см/
Из прямоугольного ΔBCH по теореме Пифагора:
b² = h² + b₁² = 6² + 18² = 36 + 324 = 360; b = √360 = 6√10
Катет BC = 6√10 см.
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.

20°
Объяснение:
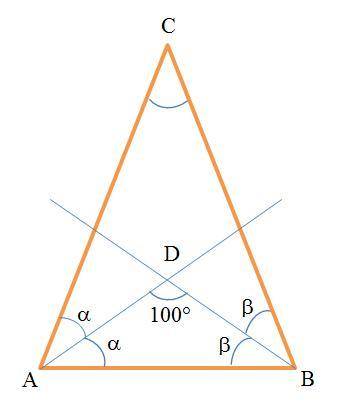
Дано (см. рисунок):
ΔАВС - равнобедренный
AD - биссектриса угла А
BD - биссектриса угла В
∠ADB = 100°
Найти: ∠С
Решение.
Так как треугольник ABC равнобедренный, то у него углы при основании равны ∠А=∠В. Биссектриса делит угол пополам, поэтому α=∠А/2 и β=∠В/2. Но ∠А=∠В и поэтому α=β. Значит, треугольник ADB также равнобедренный.
Найдём углы α и β. Сумма внутренних углов треугольника равна 180°: α + β + 100° = 180°. В силу этого α = β = (180-100)/2 = 40°.
Тогда ∠CАВ=∠СВА=2·α=2·40°=80°. Опять используем свойство:
Сумма внутренних углов треугольника равна 180°.
В силу этого ∠CАВ+∠СВА+∠С=180°. Отсюда
∠C=180°-(∠CАВ+∠СВА)=180°-(80°+80°)=180°-160°=20°.
ответ: 20°
Объяснение:
Направления север и запад - катеты прямоугольного треугольника, 3*4=12 км - длина одного катета, 4*4=16 км - длина другого катета. Расстояние между их концами - гипотенуза. По т. Пифагора - √(12²+16²)=20 км - расстояние между туристами через 4 часа.