Вгостинице города z за номер с телефоном надо доплачивать 15 р. в сутки плюс 30 к. за каждую минуту разговора. турист останавливается в гостинице на 7 дней. сколько минут он может говорить по телефону, если он планирует заплатить зп переговоры не больше 120 р.?

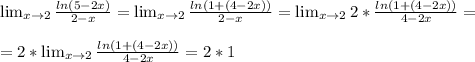
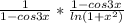
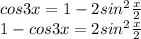
![\lim_{x \to \infty} (2-cos3x)^{ \frac{1}{ln(1+ x^{2} )} }=\lim_{x \to \infty} (1+(1-cos3x))^{ \frac{1}{ln(1+ x^{2} )} }= \\ \\ =\lim_{x \to \infty} [(1+(1-cos3x))^{\frac{1}{1-cos3x}} ]^{ \frac{1-cos3x}{ln(1+ x^{2} )} }= \\ \\ =\lim_{x \to \infty} [(1+(1-cos3x))^{\frac{1}{1-cos3x}} ]^{\lim_{x \to \infty} \frac{1-cos3x }{ln(1+ x^{2} )} }= \\ \\ e^{^{\lim_{x \to \infty} \frac{1-cos3x}{ln(1+ x^{2} )} }} =](/tpl/images/0798/7674/23b3b.png)
