Найдите периметр трапеции, если ее основания равны 8 см и 12 см, боковые стороны равны, а диагональ - id1574760420210519 от fox2457667 19.05.2021 05:32

Question

Геометрия: Найдите периметр трапеции, если ее основания равны 8 см и 12 см, боковые стороны равны, а диагональ делит острый угол трапеции пополам.

fox2457667 · Accepted Answer

Пусть центр верхнего основания O, а ABCD - это плоскость сечения. Отрезок AB принадлежит верхнему основанию, CD - нижнему. Так как рассматриваемая фигура - цилиндр, то AD=BC=6см

Чтобы найти площадь сечения, надо найти AB.

Рассмотрим верхнее основание. Построим из точки O перпендикуляр к отрезку AB. Пусть K - точка пересечения перпендикуляра и AB. По условию, OK=6см

А так как треугольник AOB - равнобедренный, то AK=BK

Рассмотрим треугольник OAK. Он прямоугольный, угол AKO=90 градусов

По теореме Пифагора

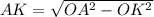
$AK=\sqrt{OA^2-OK^2}$

Из условия задачи OA=10см

Находим AK:

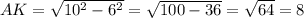
$AK=\sqrt{10^2-6^2}=\sqrt{100-36}=\sqrt{64}=8$

AB=2*AK=16см

Находим площадь сечения:

S=AB*AD=16*6=96см^2

ответ: площадь сечения равна 96см^2.

Найдите периметр трапеции, если ее основания равны 8 см и 12 см, боковые стороны равны, а диагональ делит острый угол трапеции пополам.

MOGZ ответил