Два конуса.
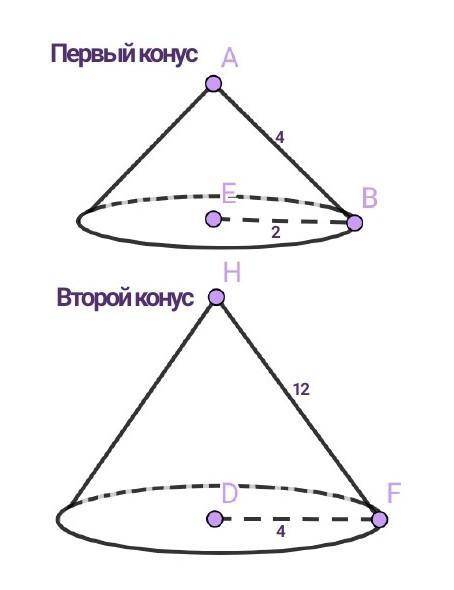
ЕВ — радиус основания первого конуса = 2.
АВ — образующая первого конуса = 4.
DF — радиус основания второго конуса = 4.
HF — образующая второго конуса = 12.
Найти:S(боковой поверхности второго конуса) / S(боковой поверхности первого конуса) = ?
Решение:[Площадь боковой поверхности конуса равна произведению π, радиуса основания конуса и образующей конуса].
То есть —
S(боковой поверхности первого конуса) = π*ЕВ*АВ = π*2*4 = 8 (ед²)*π.
S(боковой поверхности второго конуса) = π*DF*HF = π*4*12 = 48 (ед²)*π.
Тогда —
S(боковой поверхности второго конуса) / S(боковой поверхности первого конуса) = (48 (ед²)*π) / (8 (ед²)*π) = 6.
ответ:в 6 раз.
Отрезок BC виден из точек С1 и B1 под прямым углом - точки B, C1, B1, C лежат на окружности c центром в середине BC.
B1BC1 =C1CB1
A1BC1H, A1CB1H - вписанные четырехугольники (т.к. противоположные углы прямые).
HA1C1 =HBC1, HA1B1=HCB1 => HA1C1=HA1B1
(т.е. высота AA1 треугольника ABC является биссектрисой угла A1 ортотреугольника A1B1C1)
∪B1C1 =2B1BC1 =A1 =44
Если треугольник остроугольный, найдем BAC как угол между секущими:
BAC =∪BC/2 -∪B1C1/2 =90-22 =68
Если треугольник тупоугольный - рассмотрим △HBC - найдем BHC как угол между хордами:
BHC =∪BC/2 +∪B1C1/2 =90+22 =112
---------------------------------
М - середина BC. B1MC1 =∪B1C1 (центральный угол) =A1, т.е. M лежит на описанной окружности △A1B1C1.
Аналогично для всех середин сторон △ABC и середин сторон △AHB, △BHC, △AHC (для этих треугольников △A1B1C1 является ортотреугольником).
Описанная окружность ортотреугольника называется окружностью девяти точек или окружностью Эйлера (основания высот, середины сторон и середины отрезков от ортоцентра до вершины лежат на одной окружности).