У чотирикутнику CDEF, у який можна вписати коло, CD = 6 см, DE = 8 см, EF = 12 см. Знайдіть сторону CF. 2. Яку властивість повинні мати діагоналі ромба, щоб навколо нього можна було описати коло? Відповідь обґрунтуйте.
3. Кут при вершині рівнобедреного трикутника дорівнює 56°. На бічній стороні трикутника як на діаметрі побудовано півколо, яке інші сторони трикутника ділить на 3 дуги. Знайдіть градусні міри утворених дуг.
4. На малюнку точка О – центр кола. Знайдіть градусну міру дуги х.

5. На малюнку точка О – центр кола. Знайдіть кут х.

6. За даними малюнка знайдіть кут х.

7)
Чи є рівними вписані кути, сторони яких перетинають коло в двох даних точках. Відповідь обґрунтуйте.
будь ласка до ть
В четырехугольнике CDEF, в который можно вписать окружность, CD = 6 см, DE = 8 см, EF = 12 см. Найдите сторону CF.
2. Какое свойство должны иметь диагонали ромба, чтобы вокруг него можно было описать круг? ответ обоснуйте.
3. Угол при вершине равнобедренного треугольника равен 56 °. На боковой стороне треугольника как на диаметре построена полукруг, другие стороны треугольника делит на 3 дуги. Найдите градусные меры образованных дуг.
4. На рисунке точка В - центр круга. Найдите градусную меру дуги х.

5. На рисунке точка В - центр круга. Найдите угол х.

6. По данным рисунка найдите угол х.

7)
Или равны вписанные углы, стороны которых пересекают круг в двух данных точках. ответ обоснуйте.
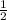·9·24=108см², а периметр 54 см.
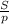где р - полупериметр r=4 см
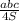R= 12,5 см
h=S/(½*a)=48/(0.5*12)=48/6=8 см
2) Т.к. треугольник равнобедренный, то высота делит его основание пополам, т.е. основание (обозначим его AO) одного из двух прямоугольных треугольников равно: AO=AC/2=12/2=6 см.
3) Рассмотрим один из прямоугольных треугольников (обозначим его AOB)
Мы знаем, чему равны оба катета прямоугольного треугольника (АО=6 см, ОB=h=8 см), теперь по теореме Пифагора найдём его гипотенузу AB:
AB=√(AO²+ОС²)=√(6²+8²)=√(36+64)=√100=10 см.
Т.к. треугольник равнобедренный, то BC - тоже 10 см.
4) Периметр равнобедренного треугольника P=AB+BC+AC=10+10+12=32 см.
ответ: P=32 см