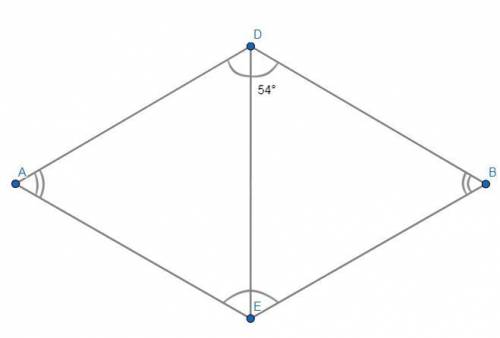
Дано:
ADBE - ромб.
DE - диагональ.
∠EDB = 54°.
Найти:
∠ADB = ?
∠DBE = ?
∠BEA = ?
∠EAD = ?
1) Диагонали ромба являются биссектрисами углов, из которых они исходят. Поэтому, ∠ADB = 2*∠EDB = 2*54° = 108°.
2) Сумма двух углов параллелограмма (ромб - частный случай параллелограмма), прилежащих к одной стороне, равна 180°. Следовательно, ∠ADB+∠DBE = 180° ⇒ ∠DBE = 180°-∠ADB ⇒ ∠DBE = 180°-108° ⇒∠DBE = 72°.
3) Противоположные углы параллелограмма равны (на рисунке выделены дугами). Следовательно, ∠ADB = ∠BEA = 108°, ∠DBE = ∠EAD = 72°.
ответ: 108°, 72°, 108°, 72°.
-----------
Соединим вершины треугольника с точкой Ѕ
АЅ=ВЅ=СЅ
Если расстояние от точки вне треугольника до его вершин одинаково., то одинаковы проекции наклонных отрезков, соединяющих эту точку с вершинами: значит, вокруг треугольника можно описать окружность, и основание перпендикуляра к плоскости треугольника лежит в центре этой описанной окружности.
По условию расстояние до плоскости треугольника 3 см
АО=R
Треугольник АОЅ- египетский, и АО=4 см( проверьте по т.Пифагора).
Радиус описанной вокруг правильного треугольника окружности равен 2/3 его высоты. ⇒
Высота треугольника АН=4:(2/3)=6 см