Решение во вложении. Я так доказывал.
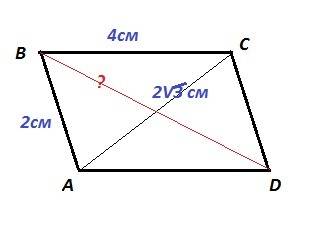
ABCD - параллелограмм. AB = 2 см, BC = 4 см, AC = 2√3 см
По теореме косинусов диагонали параллелограмма
AC² = AB² + BC² - 2 AB · BC · cos ∠B
BD² = AB² + AD² - 2 AB · AD · cos ∠A =
= AB² + AD² - 2 AB · AD · cos (180° - ∠B) =
= AB² + AD² + 2 AB · AD · cos ∠B
Так как AD = BC ⇒
BD² = AB² + BC² + 2 AB · BC · cos ∠B
Складываем почленно квадраты диагоналей.
AC² + BD² = AB² + AB² + BC² + BC²
BD² = 2 AB² + 2 BC² - AC² = 2·2² + 2·4² - (2√3)² =
= 8 + 32 - 12 = 28
BD = √28 = 2√7 см
ответ : BD = 2√7 см
Треугольник АДК=треугольнику ЕРС, как прямоугольные треугольники по двум катетам, АК=РС, ДК=ЕР, угол А=углуС , если углы при основании треугольника равны, то треугольник равнобедренный, треугольник АВС равнобедренный, АВ=ВС
Треугольник АВД и А1В1Д1 прямоугольные и равны между собой , по гипотенузе АВ=А1В1 и острому углу уголА=углуА1, значит ВД=В1Д1