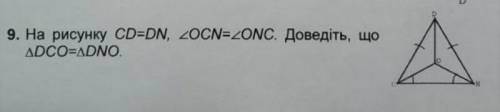
Вычисления таких задач проще простого. Сумма углов треугольника равна 180 градусов, углы при основании (beta) равны. Отсюда на все случаи углов при вершине alpha следует применять формулу
beta=(180-alpha)/2.
Если угол при вершине 110 градусов, то у основания равнобедренного треугольника углы равны
beta=(180-110)/2=35 (градусов).
Пусть задан угол при основании равнобедренного треугольника и он равен 50 градусов, тогда угол при вершине равен
alpha=180-2*50=80 (градусов).
Меняете в формуле значения угла (50) на свой и находите угол в вершине треугольника для любого равнобедренного треугольника.
По мере изучения свойств треугольника, формулы для вписанных и описанных окружностей, возрастает и сложность вычислений и разнообразие задач, которые можно решить. Таким образом в 8-9 классе задачи на треугольники требуют знаний немало важных формул без которых вычисления невозможно выполнить.
Объяснение:
лАЙК
Собственно говоря, синус – это не только математический термин. Синусами в медицине называют еще и придаточные пазухи носа. Это три парных и одна непарная воздушные полости, расположенные в черепе и непосредственно связанные с основной полостью носа. Начинают формироваться они еще внутриутробно, и развитие их продолжается на протяжении всего детства, по мере роста черепа. Понять, что такое синусит и гайморит, в чем разница между ними, и есть ли она вообще, можно, если иметь представление, зачем нужны носовые пазухи, где они расположены, как называются и почему иногда воспаляются. Именно в этих пазухах и протекают воспалительные процессы при так называемых синуситах.
Объяснение:
∠OCN=∠ONC, значит ΔCON - равнобедренный и СО=ОN
CО - общая сторона
СD=DN по условию
ΔDCO=ΔDNO по трем сторонам (3 признак равенства треугольников)