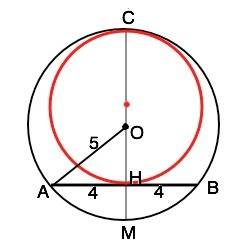
Пусть центр данной окружности О, хорда АВ, диаметр СМ перпендикулярен АВ и пересекает её в середине хорды точке Н. АН=ВН. СО=ОМ - радиусы.
Для второй окружности, хорда АВ - касательная. Следовательно, диаметр СН перпендикулярен АВ и, чтобы быть наибольшим из возможных, должен лежать на диаметре СМ данной окружности.
Соединив О и А, получим прямоугольный ∆ АОН. Этот треугольник -"египетский", катет ОН=3 ( можно проверить по т.Пифагора).
Тогда СН=СО+ОН=5+3=8. Диаметр внутренней окружности СН=8, ее радиус 8:2=4, и S=πr=16π
Треугольники А₁КА₂ подобен ΔВ₁КВ₂ по двум углам .
Угол А₁А₂К=В₁В₂К накрестлежажие при параллельных прямых А₁А₂ и В₁В₂ (лежат на параллельных плоскостях) Аналогично для углов А₂А₁К=В₂В₁К
Следовательно стороны у них будут пропорциональны
КВ₁/КА₁=КВ₂/КА₂=В₁В₂/А₁А₂=4/3
Рассмотрим КВ₁/КА₁=4/3 так как А₁В₁=7 то КВ₁=7-КА₁ получим (7-КА₁)/КА₁=4/3
21-3КА₁=4КА₁
7КА₁=21
КА₁=3 см
Рассмотрим КВ₂/КА₂=4/3 так как КА₂=12 то КВ₂/12=4/3
3КВ₂=48
КВ₂=16 см