
ЕСли АВСД - прямоугольник,
1)значит пара сторон(векторов) параллельны АВ(3-4;5-1)=АВ(-1;4)
ДС(-1-0;4-0)=ДС(-1;4)
Чтобы найти координаты вектора из координат конца вектора вычел координаты начала АВ=ДС (это векторы) раз координаты векторов равны то и векторы равны значит параллельны
2)Диагонали прямоугольника равны) - это уже длины
Сначала найду координаты векторов: АС(-1-4;4-1)=АС(-5;3)
ВД(0-3;0-5) =ВД(-3;-5)
Теперь найду длину АС=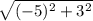 =
=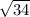 ВД=
ВД=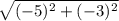 =
=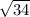
Так как АВ|| ДС; AB= СД; АС=ВД - это АВСД прямоугольник
Объяснение:
бисс., провед. к основанию, яв-ся медианой и высотой, т.е. половина основания по теорме Пифагора равна корень кв.(17(кв.)-15(кв.)=8 см., а основание тогда 16 см.
Площадь треуг. = 0,5*16*15=120 см.кв.
Периметр = 17+17=16=50 см. (так как две стороны равны по 17)
Допустим есть равнобедренный треугольник ABC, в котором АС основание, а стороны AB и BC - боковые стороны и равны 17 см. Так же есть биссектриса, проведенная к основанию (назовём её BD) равная 15 см. Рассмотрим прямоугольный треугольник АВD, в котором AB гипотенуза, а AD и BD катеты. Квадрат гипотенузы равен сумме квадратов катетов. Найдём AD. AB2 = BD2 + AD2 (2 - здесь степень) 289 = 225+AD2 => AD2=289-225 => AD2=64 => AD=8, таким образом основание AC=16. периметр равен 17+17+16=50 P=50, а площадь находим исходя из S = 1/2AB*BD S=1/2 17*15 S=120или
ОТВЕТ: P=50, S=120.