ответ:100 см²
Объяснение: В четырехугольник можно вписать окружность ( или круг) тогда и только тогда. когда суммы противоположных сторон равны.
Трапеция АВСD - четырехугольник. ⇒
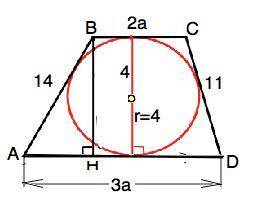
ВС+АD=АВ+AD=14+11=25 (см).
Высота трапеции равна диаметру вписанной окружности. ⇒ ВН=2r=2•4=8
Площадь трапеции равна произведению высоты и полусуммы оснований.
S=h•(a+b)/2=8•25/2=100 см².
----------------------
Как видим, для нахождения площади отношение оснований трапеции является лишним. Но для нахождения длин сторон пригодится.
Примем коэффициент отношения ВС:АD равным а.
Тогда ВС=2а, АD=3а.
ВС+АD=5a=25 (см. выше). ⇒ а=5. ⇒
ВС=2•5=10 см
АD=3•5=15 см.
Т.к. один из острых углов прямоугольного треугольника равен 45°, то и второй острый угол этого треугольника тоже равен 45°, а сам треугольник является равнобедренным ( гипотенуза является основанием равнобедренного треугольника, а катеты являются бедрами этого равнобедренного треугольника и соответственно равны друг другу )
Пусть а и b - катеты треугольника, а с - его гипотенуза. Так как в нашем случае катеты равны, то по теореме Пифагора с² = 2а²
Площадь же данного треугольника можно найти по формуле S = a*b/2
Так как в данном треугольнике катеты равны друг другу, то формула площади треугольника примет вид S = a²/2 = c²/4
Подставим численное значение длины гипотенузы в полученную формулу и найдём площадь треугольника:
S = c²/4 = 20²/4 = 400/4 = 100
Площадь данного прямоугольного треугольника равна 100.
Задача 2.
Задача 3.
Проекциями прямых параллельных сторонам исходного параллелограмма будут прямые, проходящие через т. пересечения диагоналей и середины сторон у параллелограмма проекции
Объяснение:
Дано
АВСД - прямоугольник
АВ = 6 см
АД = 2√3 см
Найти
уг. м/ду АС и ВД
Решение
Очевидно, что АС и ВД - диагонали прямоугольника.
Обозначим т. пересечения как т. О
Тогда уг.АОД - искомый угол между диагоналями.
Обозначим
По св-вам прямоугольника, его диагонали равны и в т. пересечения делятся пополам. Т.е.
АО = ОС = ВО = ОД
По Т. Пифагора можно найти диагонали:
ВД² = АВ² + АД²
BD = \sqrt{AB^2 + AD^2} \\ BD = \sqrt{6^2 + 2\sqrt(3)^2}
Соответственно
АС = ВД = 4√3Рассмотрим тогда треугольник АОД, он равнобедренный, т.к.
Так же 2√3 равна и сторона АД нашего прямоугольника.
То есть - мы получаем, что
АО = ОД = АД = 2√3
Следовательно - ∆АОД равносторонний,
а это означает, что искомый угол AOД
Для особо дотошных:
По Т. косинусов имеем:
Отсюда