Не думаю, что задачу из раздела "Геометрия 5-9" следует решать методами аналитической геометрии. Скорее как-то так (как на рисунке) ;))
Когда в тетрадке будешь рисовать- лучше взять единичный отрезок равным 3 клеточки, тогда всё точно получится. А весь рисунок при этом буде как раз по ширине тетради, а в высоту где-то 2/3 странички.
Вычислить расстояние между серединами отрезков MN и PQ. Даны координаты точек: M(1;2;1) N(3;-1;4)
P(-2;3:-3) Q(-4;-2;2)
Объяснение:
M(1;2;1) N(3;-1;4) . О-середина MN , найдем координаты О.
х(О)= ( х(M)+х(N) )/2 , х(О)= (1+3 )/2 , х(О)= 2 ; у(О)= ( у(M)+у(N) )/2 , у(О)= ( 2-1 )/2 , у(О)= 0,5;
z(О)= ( у(M)+у(N) )/2 , z(О)= ( 1+4 )/2 , z(О)= 2,5;
О( 2 ;0,5; 2,5) .
P(-2;3:-3) Q(-4;-2;2) , А-середина РQ , найдем координаты т A.
х(A)= ( х(P)+х(Q) )/2 , х(A)= (-2-4 )/2 , х(О)= -3 ; у(A)= ( у(P)+у(Q) )/2 , у(A)= ( 3-2 )/2 , у(О)= 0.5 ;
z(A)= ( у(P)+у(Q) )/2 , z(A)= ( -3-+2)/2 , z(О)= -0,5;
A( -3 ;0,5;-0,5) . .
ОА=√(-3-2)²+(0,5-0,5)²+(-0,5-2,5)²=√(25+0+9)=√34 .
1. Апофема L определяется по т Пифагора L²=h²+(a/2)²=100+4=104, L =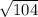
= 2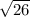
≈ 10,2 см
Объяснение:
2. Площадь основания находится как площадь равностороннего Δ с со стороной a, So =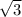 
a²/4=4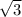. Аопофема L находится из условия L²=b²-(a/2)²=64-2,25=61,75, L ≈ 7,59 cм, тогда площадь 1 Грани = aL/2 ≈ 1,5·7,59≈11,78 cм², а вся площадь боковой поверхности = утроенной площади боковой грани ≈ 33,36 см². Общая площадь = 4√3+33,36 ≈33,36+6,93 ≈ 40,29 ≈ 40 см²
3. Диагональ основания d =6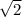
, тогда высота находится из соотношения h² = b²-(d/2)²=144-18=126, h =3
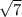, площадь основания So=a²=36, объём V=Soh/3=36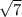≈ 95,25 ≈ 95 см²
AB: (x-0)/(3-0)=(y-1)/(5-1) => 4x=3y-3 => 4x-3y+3=0. CE: (x-6)/4=(y-0)/(-3) => -3x+18=4y =>3x+4y-18=0. D: x=(3+6)/2=9/2; y=(5+0)/2=5/2; AD: (x-0)/(9/2-0).