
Треугольники называются равными, если они совпадают при наложении. Да, это правило совершенно верно, но существует ещё одно правило про равенство треугольников...
Фигуры (в том числе и треугольники), симметричные относительно прямой, равны.
Это правило и отвечает на Ваш вопрос.
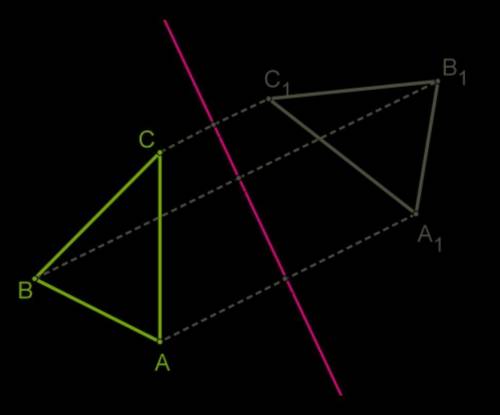
К тому же, треугольники, симметричные относительно какой-то прямой ( или оси ) совпадают при наложении. Во вложении к этому ответу есть картинка, по которой в этом можно убедиться. Если зрительно наложить один треугольник на другой, то они совпадут.
ответ:1)35°, 2)30°, 3)25°, 4)70°, 5)55°, 6)20°.
Объяснение:Если из точки вне окружности проведены две секущие или секущая и касательная, то угол между ними равен половине разности двух ,заключённых между ними дуг.
1) α=(90°-20°):2=35°; 2)(100°-х°):2=35°, 100°-х°=70°, х°=30°; ∪СД=30°.
3) α=(110°-60°):2=25°; 4)(120°-х°):2=25°, 120°-х°=50°, х°=70°; ∪СД=70°.
5) α=(70°+40°):2=55°;
Если в окружности проведены две хорды, то угол между ними будет равен половине суммы противоположных меньших дуг.
5) α=(70°+40°):2=55°; 6) (80°+х°):2=55°, 80°+х°=110°, х°=20°; ∪СД=20°.
Объяснение:
Условие перпендикулярности векторов: два вектора перпендикулярны, если их скалярное произведение равно нулю.
x₁x₂+y₁y₂+z₁z₂=0
Подставляя в уравнение данные координаты векторов решаем его относительно неизвестной координаты m.
с(-3;2;8)
b(-2;m;-3)
(-3)*(-2)+2m+8*(-3)=0
6+2m-24=0
2m=18
m=9;
При m=9 векторы с и b перпендикулярны.