∡ BAC = 30
∡ BCA = 30
∡ ABC =120
Объяснение:
Высота BD образует прямоугольные треугольники ABD и DBC. Рассмотрим один из них (ABD) в нем:
АВ = 29.8 см
BD = 14.9 см
АВ - гипотенуза. Известно, что если сторона прямоугольного треугольника равна половине гипотенузе, то эта сторона лежит против угла 30 градусов, следовательно, угол ВАС = 30 градусов
треугольник АВС равнобедренный, значит углы при основании равны, т.е АСВ=ВАС = 30 градусов
сумма углов треугольника = 180 градусов, следовательно АВС = 180 - 30-30 = 120
Объяснение:
1.
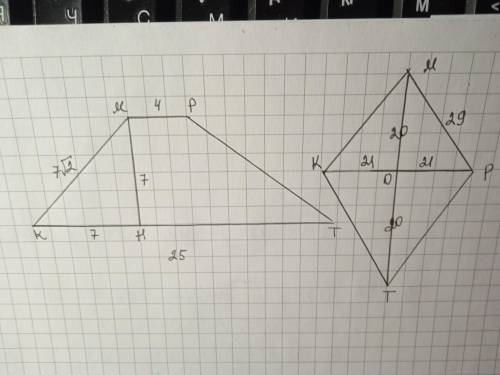
Дано: КМРТ - трапеция, МР=4; КТ=25; ∠М=135°; КМ=7√2. S(КМРТ) - ?
Проведем высоту МН, ΔКМН - прямоугольный, ∠КМН=135-90=45°, значит ∠К=45° и КН=МН.
По теореме Пифагора КМ=√(КН²+МН²); пусть КН=МН=х, тогда
(7√2)²=х²+х²; 2х²=98; х²=49; х=7. МН=7.
S=(МР+КТ):2*МН=(4+25):2*7=101,5 ед²
2.
Дано КМРТ - ромб, МР=29; КР=42. S(КМРТ) - ?
Стороны ромба равны. Диагонали ромба образуют прямой угол и в точке пересечения делятся пополам.
ΔМОР - прямоугольный, МР=29; ОР=42:2=21.
По теореме Пифагора МО=√(МР²-ОР²)=√(841-441)=√400=20.
МТ=20*2=40.
S=1/2 * КР * МТ = 1/2 * 40 * 42 = 840 ед²
Площадь параллелограмма находится по формуле S=а*b*sin угла между a и b (где a и b - стороны параллелограмма). Подставляем, то что дано в формулу 24=a*b*sin30 (sin30=0,5). Тогда получим 24=a*b*0,5, 48=a*b. Далее примем одну из сторон параллелограмма за х, тогда вторая сторона будет равна 3х, подставляем в равенство 48=a*b, получаем 48=х*3х, 48=3*х в квадрате, 16=х в квадрате, х=4 (это одна из сторон). Тогда вторая сторона 3*4=12. Периметр=2*4+2*12=32.