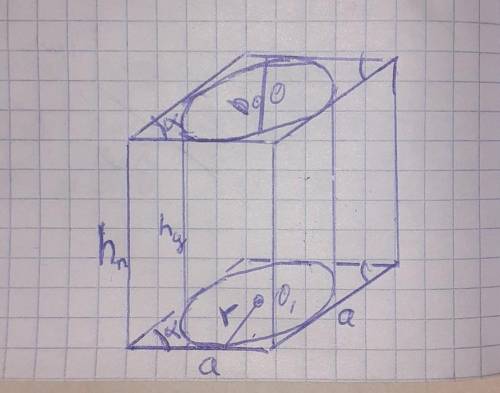
Объяснение:
α=45°
hп=15см
Sб.п. цилиндр =90π см²
найти Sб.п. призмы - ?
высота призмы равна высоте цилиндра
hп=hц=15см
площадь боковой поверхности цилиндра
Sб.п.ц=2πrhц отсюда радиус цилиндра
r=Sб.п.ц / 2πhц=90π / 2×π×15=90π / 30π=3 см
высота ромба лежащего на основании призмы равна диаметру вписанной окружности или двум радиусам окружности hр=D=2r.
формула радиуса вписанной окружности в ромб через острый угол выглядит так
r=a×sinα/2 , где сторона ромба а
отсюда сторона ромба
а=2r/sinα=2×3/sin(45°)=6 ÷ √2/2=6×2/√2=12/√2 см
чтобы найти площадь боковой поверхности призмы
сначала находим периметр основания .
так как в основании призмы ромб, ромб имеет n=4 равные стороны. периметр основания
Р=n×a=4×12/√2=48/√2 см
площадь боковой поверхности призмы
Sб.п.призма =Р×h=48/√2 ×15=720/√2 см²
TMNK- равнобедренная трапеция вписана окружность. Площадь трапеции 125. Хорда, параллельная основаниям , проведена в точки касания боковых сторон и равна 8. Найдите площадь круга.
Объяснение:
S(круга)= π R². R-?
1) Пусть О-центр вписанной окружности, ОА=ОР=ОY=R.
S (трапеции) =1/2*h*(a+b) , h=2R , (a+b)/2- длина средней линии.
2) Проведем среднюю линию НС. Она будет параллельна АВ, и пройдет через центр О (по свойству противоположных сторон описанного четырехугольника)
3) Т.к АВ параллельна основаниям , то ∠АХО=90° , тк радиус проведенный в точку касания перпендикулярен касательной.
ΔАХО-прямоугольный , cos∠ОАХ=АХ/АО , cos∠ОАХ=4/R
4) ∠ОАХ=∠АОН , тк АХ|| НО , АО-секущая.
ΔАОН-прямоугольный, cos∠ОАН=АО/НО, 4/R= R/НО ,4HO=R², 2(2HO)=R², HC=R²/2,
5) S (трапеции) =1/2 *(a+b) *h или 125= R²/2*2R , 125=R ³, R=5
S(круга)= 25π ед².