Вы, возможно, ошиблись в условии, и нужно найти площадь треугольника АВС, а не АВD?
Иначе для чего дана длина стороны ВС и отрезка DС? Сделаем рисунок к задаче.
Рассмотрим ⊿ ВDС.
Катет ВD=12 см, гипотенуза ВС=13 см.
С отрезком DС основания они составляют "египетский" треугольник, поэтому этот отрезок равен 5 см.
Треугольник АВD - также прямоугольный, а так как угол А=45°, он и равнобедренный.
Отрезок АD основания равен высоте ВD=12 см
Основание АС треугольника АВС равно
АС=АD+DС=12+5=17 см
S ᐃ АВС=ВD·АС⠰2=102 см²
1) параллелограмм АВСД, диагональ АС соединяет острые углы, она же по условию и биссектриса, значит,
уг. ВАС = уг.ДАС
т.к. это параллелограмм, то стороны АД и ВС - параллельны, а значит,
уг. ДАС = уг ВСА , следовательно в треугольнике АВС углы ВАС = ВСА - т.е. он равнобедренный, т.е. АВ=ВС .
т.к. в параллелограмме противоположные стороны рваны, то
АВ = СД и ВС = АД, и значит, АВ=ВС=СД=АД - это ромб.
2) в трапеции АВСД, углы В и С - тупые, из них проведены биссектрисы ВН и СН и т.к. по условиям они пересекаются на другом основании, то Н - точка на стороне АД
т.к. ВН - биссектрисса, то уг. АВН = уг. СВН
т.к. АВСД - трапеция, то АД параллельно ВС, и значит, уг. СВН = ВНА
следовательно в треугольнике АВН углы ВНА = АВН - т.е. он равнобедренный, т.е. АВ=АН .
аналогично, получаем ,что треугольник СДН тоже равнобедренный и СД=ДН
т.к. АД = АН+ДН , то получаем искомое:
АД = АВ + СД
Находим длины отрезков ЕD и ЕС:
обозначим АЕ за , тогда
, тогда 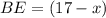
Пересекающиеся хорды окружности обладают таким свойством:
При пересечении двух хорд окружности, получаются отрезки, произведение которых у одной хорды равно произведению отрезков другой хорды.
Используя это свойство, составляем уравнение: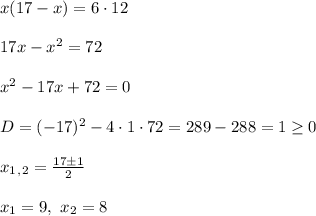
Оба корня и являются решением, поскольку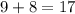
ответ: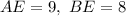
Ну и, как "Лучшее решение" не забудь отметить, ОК?!... ;)))