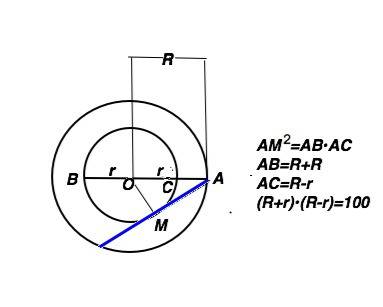
1) Через две точки можно провести только одну прямую (аксиома).
При расположении точек важно, чтобы ни одни три не располагались на одной прямой.
Как вариант построения:
Наложите два треугольника один на другой так, чтобы они не имели общих вершин и их стороны пересекались. Вершины треугольников можно попарно соединять в разных комбинациях (см. рисунок в приложении)
2) Через любые две точки проходит одна и только одна прямая. (Аксиома).
Пересекающиеся прямые имеют только одну общую точку. В противном случае , если бы они имели две общие точки, то через эти точки проходили бы две различные прямые, что противоречит аксиоме.
Отсюда следуют варианты:
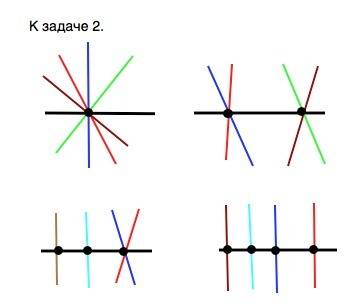
а) все четыре прямые пересекают данную в одной точке.
б) прямые пересекают её в двух точках ( по две в каждой)
в) в трёх точках ( две из них пересекают прямую в одной точке)
г) в четырех точках -каждая прямая пересекает данную в отдельной точке.
При пересечении четырех прямых с данной может образоваться от одной до четырех точек пересечения.

пусть x-длина, тогда b-ширина.
составляешь систему:
ab=56 (площадь)
2(a+b)=30... если сократить на 2, то получается a+b=15
выражаешь отсюда a.
a=15-b
подставляешь в перое уравнение вместе a
получается:
b(15-b)=56
15b-b^2-56=0
решаешь квадратное уравнение и находишь b. (одно из корней будет отрицательным, оно не соответствует условию, т.к. ширина не может быть отрицательной)
и дальше, если b=?, то, a=15-b
найдя длину и ширину, смотришь, на сколько длина больше ширины