V=1/3* S * h
S = √18(18-13)(18-13)(18-10) = √18(5*5*8)=√3600=60
h=9
V=1/3 * 60 * 9= 180 см
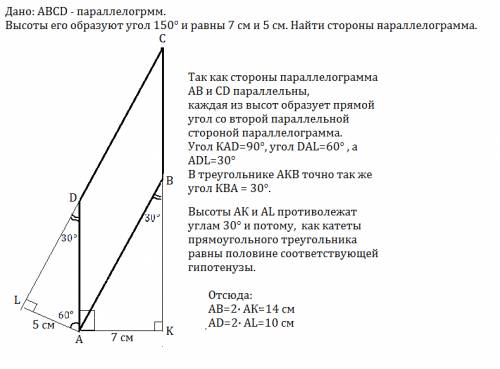
Дано: АВСD - параллелогрмм.
Высоты его образуют угол 150° и равны 7 см и 5 см.
Найти стороны параллелограмма.
Сделаем рисунок.
Так как высоты проведены из вершины острого угла,
их основания лежат на продолжении сторон ВС и СD параллелограмма .
Проведем эти высоты и обозначим их АК и АL
По условию угол KAL равен 150°.
Так как стороны параллелограмма АВ и CD параллельны,
каждая из высот образует прямой угол со второй параллельной стороной параллелограмма.
Угол КАD=90°, угол DAL=60° , а ADL=30°
В треугольнике АКВ точно так же угол КВА = 30°.
Высоты АК и АL противолежат углам 30° и потому, как катеты прямоугольного треугольника равны половине соответствующей гипотенузы.
Отсюда:
АВ=2· АК=14 см
АD=2· AL=10 см
1) из вершины тупого угла, равен острому углу параллелограмма:
Из вершины опущены две высоты: одна на противоположную сторону h1 идругая на смежную сторону h2. Через точку основания h2 проведём прямую перпендикулярную высоте h1. Вседствии чего у нас образуется три подобных прямоугольных треугольника из них следует утверждение, что угол между высотами = острому углу паралелограмма.( там сплош паралели и перпендикуляры) Когда Вы начертете рисунок всё бросится в глаза.
2) острого угла, равен тупому углу параллелограмма: Высоты будут опущены на продолжение сторон паралелограмма. Опять рассматриваем три подобных прямоугольных треугольника, один из которых рассматривали в первом случае.
Угол между внешними высотами = равен тупому углу паралеллограмма.
Площадь треугольника = корень(p x (p-a) x (p-b) x (p-c)), где р -полупериметр, остальное стороны
Полупериметр = (13+13+10)/2=18
Площадь треугольника=корень (18 х (18-13) х (18-13) х (18-10)) = корень 3600=60
Объем = 1/3 площади основания х высоту = 1/3 х 60 х 9 = 180