Пусть R, r -- радиусы двух окружностей, O₁, O₂ -- их центры.
1. Взаимное расположение двух окружностей
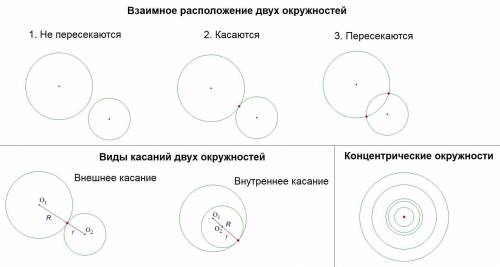
Выделяют три основных случая взаимного расположения окружностей:
Две окружности не имеют общих точек (не пересекаются)Две окружности имеют одну общую точку (касаются)Две окружности имеют две общие точки (пересекаются)Также выделяют иногда четвёртый случай: совпадающие окружности (бесконечное множество общих точек).
2. В каком случае окружности имеют одну общую точку?
Окружности будут иметь одну общую точку, если:
Сумма их радиусов равна расстоянию между центрами (R + r = O₁O₂).Разность их радиусов равна расстоянию между центрами (R - r = O₁O₂).3. Как называется общая точка двух окружностей?
Если окружности касаются в некоторой точке, то такая точка называется точкой касания.
Если пересекаются -- точкой пересечения.
4. Виды касаний двух окружностей
В пункте 2 было выделено два признака касания окружностей, откуда получается 2 вида касания:
Внешнее касание (R + r = O₁O₂)Внутреннее касание (R - r = O₁O₂)5. Когда окружности пересекаются?
Окружности пересекаются, когда расстояние между центрами меньше суммы радиусов, но больше их разности: R - r < O₁O₂ < R + r
6. Концентрические окружности
Окружности, имеющие общий центр, называются концентрическими.
Перпендикулярным отрезком, проведенным из точки к данному прямой называют перпендикуляром .
Теорема — утверждение, справедливость которого устанавливается путем рассуждения, а сами рассуждения — доказательством теоремы
Условие — это начало теоремы, а заключение — конец теоремы
Теорема о перпендикуляре , проведенным из точки к данной прямой: из точки, не лежащей на данной прямой, можно провести перпендикуляр к этой прямой, и притом только один
Медиана треугольника— это отрезок,соединяющий вершину треугольника с серединой противоположной стороны
Любой треугольник имеет три медианы.
Биссектриса треугодиника — отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны
Любой треугольник имеет три биссектрисы.
Высота треугольника — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Любой треугольник имеет три высоты.
Равнобедренным треугольником называется треугольник, у которого две его стороны равны.
Стороны равнобедренного треугольника называют боковыми сторонами.
Равносторонний треугольник — это треугольник, у которого все стороны равны.
Свойство : все углы равностороннего треугольника равны.
Теорема об углах равнобедренного треугольника: В равнобедренном треугольнике углы при основании равны.
Теорема о биссектрисе равнобедренного треугольника: в равнобедренном треугольнике биссектриса , проведенная к основнованию, является медианой и высотой.
Теорема о равестве треугольников: 1) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и уголу между ними другого треугольника, то такие треугольники равны.
2) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Окружность— геометрическая фигура, состаящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Данная точка — центр окружности.
Радиус — отрезок соединяющий центр окружности с какой либо точкой окружности.
Хорда — отрезок соединяющий две точки окружности
Диаметр — хорда проходящая через центр окружности