ответ: 324см²
Объяснение: диагональ основания АС делит его на 2 равных прямоугольных треугольника АВС и АСД, в которых стороны основания являются катетами а диагональ АС - гипотенуза. Найдём катет СД по теореме Пифагора:
СД²=АВ²=√(АС²-АД²)=√(13²-12²)=
=√(169-144)=√25=5см
Теперь найдём площади боковых граней, зная стороны и высоту параллелепипеда:
Sabcd=Sa1b1c1d1=5×12=60см². Таких граней 2, поэтому площадь двух таких граней=60×2=120см²
В параллелепипеде 6 граней и одинаковых по 2, поэтому будем умножать каждую найденную площадь грани на 2
Saa1b1b=Sdd1c1c=5×6=30см²; 2S=30×2=60см²
Saa1d1d=Sbb1c1c=12×6=72см²
2S=72×2=144см²
Теперь найдём полную площадь поверхности параллелепипеда, зная площиди всех его граней:
Sпол=120+60+144=324см²
ответ: 8.5
Объяснение:
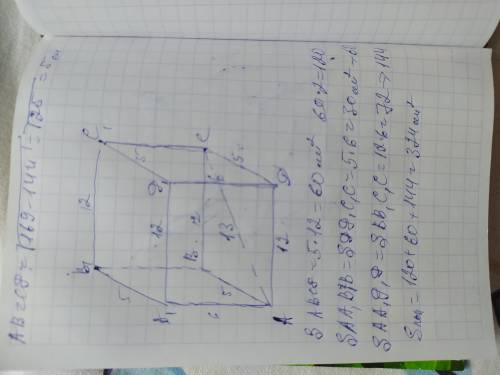
Заметим, что точка не лежит между двумя параллельными прямыми, а значит, фигура которая высекается прямыми будет трапецией в плоскости АD1D2, так как прямые параллельны. Посмотрим на рисунок в плоскости АD1D2 - это, как уже было сказано ранее, трапеция, но не простая. Известно равенство отрезков KC1 = C1D1. Рассмотрим ΔD1D2K.
В нем проведена прямая С1С2 ║основанию через середину стороны D1K(KC1 = C1D1), значит эта прямая - средняя линия треугольника ⇒точка C2 делит сторону пополам и, по свойству средней линии,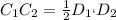 
. Находим по этой формуле C1C2. Он равен 8.5.
Такое уже можно и загуглить, что за ленивые люди, даже списать не можете